题目内容
在△ABC中，a＝3，b＝2
，∠B＝2∠A.
(1) 求cosA的值；
(2) 求c的值．
解：(1) 因为a＝3，b＝2，∠B＝2∠A.所以在△ABC中，由正弦定理得
.所以
故cosA＝
.
(2) 由(1)知cosA＝
，所以sinA＝
又因为∠B＝2∠A，所以cosB＝2cos2A－1＝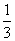
.所以sinB＝
在△ABC中，sinC＝sin(A＋B)＝sinAcosB＋cosAsinB＝
.
所以c＝
＝5.
练习册系列答案
阅读快车系列答案
相关题目
，n∈N*，其中c为实数．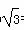
b.
，BC＝1，sinC＝
，则
＝________．
＋
.
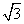上的最大值和最小值及取得最值时x的值．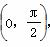
，sinα＝
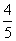，tan(α－β)＝－
，求cosβ的值．