Question

已知函数f(x)＝x²＋alnx.

(1)当a＝－2时，求函数f(x)的单调区间；

(2)若g(x)＝f(x)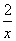＋在[1，＋∞)上是单调函数，求实数a的取值范围．

Answer 1

解　(1)由已知，函数的定义域为(0，＋∞)．

当a＝－2时，f(x)＝x²－2lnx，

所以f′(x)＝2x－＝，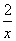

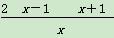则当x∈(0,1)时，f′(x)<0，

所以(0,1)为f(x)的单调递减区间．

当x∈(1，＋∞)时，f′(x)>0，(1，＋∞)为f(x)的单调递增区间．

(2)由题意得g′(x)＝2x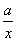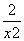＋－，函数g(x)在[1，＋∞)上是单调函数．

(ⅰ)若函数g(x)为[1，＋∞)上的单调增函数，

则g′(x)≥0在[1，＋∞)上恒成立，

即a≥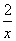－2x²在[1，＋∞)上恒成立，

设φ(x)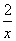＝－2x²，因为φ(x)在[1，＋∞]上单调递减，

所以φ(x)_max＝φ(1)＝0，所以a≥0.

(ⅱ)若函数g(x)为[1，＋∞)上的单调减函数，

则g′(x)≤0在[1，＋∞)上恒成立，不可能．

综上，实数a的取值范围是[0，＋∞)．