题目内容
已知Q是椭圆
+
=1上一点,P(1,-1),F1、F2分别是椭圆的左、右焦点.
(1)若QF12-QF22=4,求cos∠F1QF2的值;
(2)求QP+QF2的最大值,并求出此时Q点坐标.
| x2 |
| 4 |
| y2 |
| 3 |
(1)若QF12-QF22=4,求cos∠F1QF2的值;
(2)求QP+QF2的最大值,并求出此时Q点坐标.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用QF12-QF22=4,结合椭圆的定义,求出QF1=2.5,QF2=1.5,再利用余弦定理,即可求cos∠F1QF2的值;
(2)QP+QF2=PQ+4-QF1≤4+PF1=4+
,当且仅当P,Q,F1三点共线时,取等号,直线PF1的方程代入椭圆方程,即可求出此时Q点坐标.
(2)QP+QF2=PQ+4-QF1≤4+PF1=4+
| 5 |
解答:
解:(1)∵QF12-QF22=4,QF1+QF2=4,
∴QF1-QF2=1,
∴QF1=2.5,QF2=1.5,
∴cos∠F1QF2=
=0.6;
(2)QP+QF2=PQ+4-QF1≤4+PF1=4+
,当且仅当P,Q,F1三点共线时,取等号.
∴QP+QF2的最大值为4+
.
直线PF1的方程为y=-
(x+1),代入椭圆方程可得4x2+2x-11=0,
可得x=
(另一根舍去),
∴y=
,
∴Q(
,
).
∴QF1-QF2=1,
∴QF1=2.5,QF2=1.5,
∴cos∠F1QF2=
| 2.52+1.52-4 |
| 2•2.5•1.5 |
(2)QP+QF2=PQ+4-QF1≤4+PF1=4+
| 5 |
∴QP+QF2的最大值为4+
| 5 |
直线PF1的方程为y=-
| 1 |
| 2 |
可得x=
-1-3
| ||
| 4 |
∴y=
3
| ||
| 8 |
∴Q(
-1-3
| ||
| 4 |
3
| ||
| 8 |
点评:本题考查椭圆的方程与定义,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
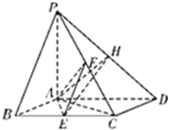 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=AB=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=AB=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点