题目内容
9．口袋中有100个大小相同的红球、白球、黑球，其中红球45个，从口袋中摸出一个球，摸出白球的概率为0.23，则摸出黑球的概率为（ ）| A． | 0.32 | B． | 0.45 | C． | 0.64 | D． | 0.67 |
分析 先求出口袋中有100-45-0.23×100=32个黑球，由此能求出摸出黑球的概率．
解答 解：∵口袋中有100个大小相同的红球、白球、黑球，其中红球45个，
从口袋中摸出一个球，摸出白球的概率为0.23，
∴口袋中有100-45-0.23×100=32个黑球，
∴摸出黑球的概率为p=$\frac{32}{100}=0.32$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
19．
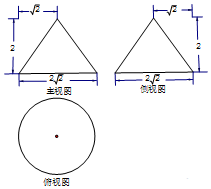某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则新工件的棱长为（ ）
某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则新工件的棱长为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | $2-\sqrt{2}$ |
14．在△ABC中，AB=AC=1，$\overrightarrow{AM}$=$\overrightarrow{MB}$，$\overrightarrow{BN}$=$\overrightarrow{NC}$，$\overrightarrow{CM}$•$\overrightarrow{AN}$=-$\frac{1}{4}$，则∠ABC=（ ）
| A． | $\frac{5π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
18．已知a=2ln3，b=2lg2，c=（$\frac{1}{4}$）${\;}^{lo{g}_{\frac{1}{3}}\frac{1}{2}}$，则（ ）
| A． | c＞a＞b | B． | a＞b＞c | C． | a＞c＞b | D． | b＞c＞a |