题目内容
14.在△ABC中,AB=AC=1,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{BN}$=$\overrightarrow{NC}$,$\overrightarrow{CM}$•$\overrightarrow{AN}$=-$\frac{1}{4}$,则∠ABC=( )| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 由题意画出图形,利用已知条件求出∠BAC=$\frac{π}{2}$,可得∠ABC=$\frac{π}{4}$.
解答 解:如图,
∵AB=AC=1,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{BN}$=$\overrightarrow{NC}$,$\overrightarrow{CM}$•$\overrightarrow{AN}$=-$\frac{1}{4}$,
∴$\overrightarrow{CM}$•$\overrightarrow{AN}$=($\overrightarrow{AM}$-$\overrightarrow{AC}$)•$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$)•$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
=$\frac{1}{4}$|$\overline{AB}$|2+$\frac{1}{4}\overrightarrow{AB}$•$\overrightarrow{AC}$-$\frac{1}{2}\overrightarrow{AB}$•$\overrightarrow{AC}$-$\frac{1}{2}$|$\overrightarrow{AC}$|2=$\frac{1}{4}$-$\frac{1}{4}$cos∠BAC-$\frac{1}{2}$=-$\frac{1}{4}$,解得cos∠BAC=0,
则∠BAC=$\frac{π}{2}$.
∴∠ABC=$\frac{π}{4}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查了向量加法、减法的三角形法则,是中档题.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | 0.32 | B. | 0.45 | C. | 0.64 | D. | 0.67 |
| A. | k≥1 | B. | k>1 | C. | 0<k<1 | D. | 0<k≤1 |
| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{2}{5}$ |
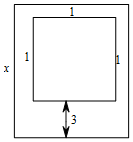 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?