题目内容
2.函数f(x)的图象上任意一点A(x,y)的坐标满足条件|x|≥|y|,称函数f(x)具有性质P,下列函数中,具有性质P的是( )| A. | f(x)=x2 | B. | f(x)=$\frac{1}{{x}^{2}+1}$ | C. | f(x)=sinx | D. | f(x)=ln(x+1) |
分析 不等式|x|≥|y|表示的平面区域如图所示,函数f(x)具有性质P,则函数图象必须完全分布在阴影区域①和②部分,由此能求出结果
解答 解:不等式|x|≥|y|表示的平面区域如图所示 :
:
函数f(x)具有性质P,则函数图象必须完全分布在阴影区域①和②部分,
在A中,f(x)=x2图象分布在区域①②和③内,故A不具有性质P;
在B中,$f(x)=\frac{1}{{x}^{2}+1}$图象分布在区域②和③内,故B不具有性质P;
在C中,f(x)=sinx图象分布在区域①和②内,故C具有性质P;
在D中,f(x)=ln(x+1)图象分布在区域②和④内,故D不具有性质P.
故选:C.
点评 本题考查函数是否具有性质P的判断,是基础题,解题时要认真审题,注意函数性质、数形结合思想的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
12.数集P={x|x=(2n+1)π,n∈Z}与数集Q={x|x=(4m±1)π,m∈Z}之间的关系是( )
| A. | P⊆Q | B. | P=Q | C. | Q⊆P | D. | P≠Q |
13.直线$\left\{{\begin{array}{l}{x={x_0}+tcosα}\\{y={y_0}+tsinα}\end{array}}\right.$(t为参数,α是直线的倾斜角)上有两点P1,P2,它们所对应的参数值分别是t1,t2,则|P1P2|等于( )
| A. | t1+t2 | B. | |t1|+|t2| | C. | |t1+t2| | D. | |t1-t2| |
10.如图茎叶图中有8个数字,茎为十位数,叶为个位数,则这组数据的中位数是( )


| A. | 91 | B. | 92 | C. | 91.5 | D. | 80.25 |
17.双曲线y2-$\frac{{x}^{2}}{3}$=1的焦点坐标是( )
| A. | (0,$\sqrt{2}$),(0,-$\sqrt{2}$) | B. | ($\sqrt{2}$,0),($-\sqrt{2}$,0) | C. | (0,2),(0,-2) | D. | (2,0),(-2,0) |
14.某同学利用课余时间做了一次社交软件使用习惯调查,得到2×2列联表如下:
则下列结论正确的是( )
| 偏爱微信 | 偏爱QQ | 合计 | |
| 30岁以下 | 4 | 8 | 12 |
| 30岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| A. | 在犯错误的概率不超过0.005的前提下认为社交软件使用习惯与年龄有关 | |
| B. | 在犯错误的概率超过0.005的前提下认为社交软件使用习惯与年龄有关 | |
| C. | 在犯错误的概率不超过0.001的前提下认为社交软件使用习惯与年龄有关 | |
| D. | 在犯错误的概率超过0.001的前提下认为社交软件使用习惯与年龄有关 |
11.已知$sin(α+\frac{π}{2})=\frac{3}{5}$,0<α<π,则sin2α的值等于( )
| A. | $\frac{12}{25}$ | B. | $-\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
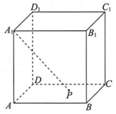 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.