题目内容
12．若复数z=$\frac{3}{1+2i}$（i是虚数单位），则$\frac{4i}{z•\overline{z}-1}$=（ ）| A． | i | B． | 2i | C． | 3i | D． | 5i |
分析 利用复数的运算法则化简复数z，利用共轭复数的性质可得：$z•\overline{z}$，进而得出．
解答 解：复数z=$\frac{3}{1+2i}$=$\frac{3（1-2i）}{（1+2i）（1-2i）}$=$\frac{3}{5}$-$\frac{6}{5}$i，
$z•\overline{z}$=$（\frac{3}{5}）^{2}+（-\frac{6}{5}）^{2}$=$\frac{9}{5}$．
则$\frac{4i}{z•\overline{z}-1}$=$\frac{4i}{\frac{9}{5}-1}$=5i．
故选：D．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
2．函数f（x）的图象上任意一点A（x，y）的坐标满足条件|x|≥|y|，称函数f（x）具有性质P，下列函数中，具有性质P的是（ ）
| A． | f（x）=x2 | B． | f（x）=$\frac{1}{{x}^{2}+1}$ | C． | f（x）=sinx | D． | f（x）=ln（x+1） |
20．函数f（x）=x2+cosx的导数f′（x）为（ ）
| A． | x-sinx | B． | 2x-sinx | C． | x+sinx | D． | 2x+sinx |
17．
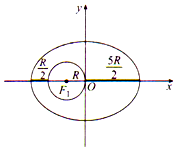我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）| A． | $\frac{2}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |
2．
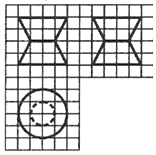如图，网格纸上小正方形的边长为1，图中粗线画出的是某零件的三视图，该零件由一个底曲直径为4，高为4的圆柱体毛坯切削得到，削切削掉部分的体积与原毛坯体积的比值为（ ）
如图，网格纸上小正方形的边长为1，图中粗线画出的是某零件的三视图，该零件由一个底曲直径为4，高为4的圆柱体毛坯切削得到，削切削掉部分的体积与原毛坯体积的比值为（ ）| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{5}{12}$ | D． | $\frac{7}{12}$ |