题目内容
7．
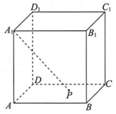如图，正方体ABCD-A1B1C1D1的棱长为2，点P在正方形ABCD的边界及其内部运动．平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成，则W的面积是$\frac{π}{4}$．
分析 可得P的轨迹就是以A1为球心的球面与面ABCD的交线．即以A为圆心，半径为1的$\frac{1}{4}$圆面
解答 解：通过作图，当A1P=$\sqrt{5}$时，分析得到P在以A1为球心，以$\sqrt{5}$为半径的球面上，又点P在正方形ABCD的边界及其内部运动，由此可得P的轨迹就是球与面ABCD的交公共部分，即以A为圆心，半径为1的$\frac{1}{4}$圆面，其面积为$\frac{1}{4}π{r}^{2}=\frac{π}{4}$．
故答案为：$\frac{π}{4}$
点评 本题考查了空间轨迹问题，考查了学生的空间想象能力，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
17．为了了解青少年的肥胖情况是否与常喝碳酸饮料有关，现对30名青少年进行调查，得到如下列联表：
已知从这30名青少年中随机抽取1名，抽到肥胖青少年的概率为$\frac{4}{15}$．
（1）请将上面的列联表补充完整．
（2）是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关？
（3）若这30名青少年中，常喝碳酸饮料且肥胖的有2名女生，则从常喝碳酸饮料且肥胖的青少年中随机抽取2名，恰好抽到一男一女的概率是多少？
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a-b）（c+d）（a-c）（b+d）}$，其中n=a+b+c+d）
| 常喝 | 不常喝 | 总计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总计 | 30 |
（1）请将上面的列联表补充完整．
（2）是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关？
（3）若这30名青少年中，常喝碳酸饮料且肥胖的有2名女生，则从常喝碳酸饮料且肥胖的青少年中随机抽取2名，恰好抽到一男一女的概率是多少？
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a-b）（c+d）（a-c）（b+d）}$，其中n=a+b+c+d）
| p（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
2．函数f（x）的图象上任意一点A（x，y）的坐标满足条件|x|≥|y|，称函数f（x）具有性质P，下列函数中，具有性质P的是（ ）
| A． | f（x）=x2 | B． | f（x）=$\frac{1}{{x}^{2}+1}$ | C． | f（x）=sinx | D． | f（x）=ln（x+1） |
16．已知函数f（x）=x（1+|x|），设关于x的不等式f（x2+1）＞f（ax）的解集为A，若$[-\frac{1}{2}，\frac{1}{2}]⊆A$，则实数a的取值范围为（ ）
| A． | （-2，2） | B． | $（-\frac{5}{2}，\frac{5}{2}）$ | C． | $（-\frac{5}{2}，-1）∪（1，\frac{5}{2}）$ | D． | $（-∞，-\frac{5}{2}）∪（\frac{5}{2}，+∞）$ |
17．
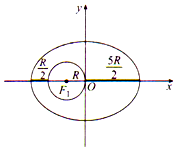我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）| A． | $\frac{2}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |