题目内容
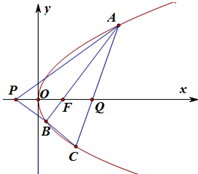已知抛物线y2=4x的焦点F，过F作直线l交抛物线于A（xA，yA），B（xB，yB）两点，其中点A在x轴上方．（1）求yAyB的值，当|AB|=8时，求直线l的方程；
（2）设P（-1，0），求证：直线PA，PB的斜率之和为0；
（3）设Q（2，0），AQ的延长线交抛物线于C，BC的中点为D，当直线DF在y轴上的截距的取值范围是（
| 2 |
| 3 |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）设l：y=k（x-1），由
，得y2-
y-4=0，由韦达定理和椭圆弦长公式能求出直线l的方程．
（2）由yAyB=-4，和得kPA+kPB=
+
=0，由此能证明直线PA，PB的斜率之和为0．
（3）由（1）得C（
，
），B（
，
），从而D（
，
），DF：y=
（x-1），由此能求出yA取值范围．
|
| 4 |
| k |
（2）由yAyB=-4，和得kPA+kPB=
| yA |
| xA+1 |
| yB |
| xB+1 |
（3）由（1）得C（
| 16 |
| yA2 |
| -8 |
| yA |
| 4 |
| yA2 |
| -4 |
| yA |
| 10 |
| yA2 |
| -6 |
| yA |
| 6yA |
| yA2-10 |
解答：
（1）解：由直线与抛物线有两个不同交点知直线l的斜率不为零，
当直线l的斜率存在且不为零时，设l：y=k（x-1），
由
，得y2-
y-4=0，
∴yAyB=-4，yA+yB=
，
当l斜率不存在时，yAyB=-4，∴yAyB=-4，
|AB|=
|y1-y2|=
=8，
解得k=±1，
∴直线l的方程为：y=x-1或y=x+1．
（2）证明：∵yAyB=-4，
∴kPA+kPB=
+
，
=
=0，
∴直线PA，PB的斜率之和为0．
（3）解：由（1）得C（
，
），B（
，
），
∴D（
，
），∴DF：y=
（x-1），
令x=0，得
∈(
，2)，∴yA∈（1，2），
∴yA取值范围是（1，2）．
（1）解：由直线与抛物线有两个不同交点知直线l的斜率不为零，当直线l的斜率存在且不为零时，设l：y=k（x-1），
由
|
| 4 |
| k |
∴yAyB=-4，yA+yB=
| 4 |
| k |
当l斜率不存在时，yAyB=-4，∴yAyB=-4，
|AB|=
1+
|
1+
|
| (y1+y2)2-4y1y2 |
解得k=±1，
∴直线l的方程为：y=x-1或y=x+1．
（2）证明：∵yAyB=-4，
∴kPA+kPB=
| yA |
| xA+1 |
| yB |
| xB+1 |
=
(yA+yB)(1+
| ||
| (xA+1)(xB+1) |
∴直线PA，PB的斜率之和为0．
（3）解：由（1）得C（
| 16 |
| yA2 |
| -8 |
| yA |
| 4 |
| yA2 |
| -4 |
| yA |
∴D（
| 10 |
| yA2 |
| -6 |
| yA |
| 6yA |
| yA2-10 |
令x=0，得
| -6yA |
| yA2-10 |
| 2 |
| 3 |
∴yA取值范围是（1，2）．
点评：本题考查直线方程的求法，考查两直线的斜率之和为0的证明，考查点的纵坐标的取值范围的求法，解题时要认真审题，注意椭圆弦长公式的合理运用．
练习册系列答案
快捷英语周周练系列答案
相关题目