题目内容
设函数f(x)定义于闭区间[0,1],满足f(0)=0,f(1)=1,且对任意x,y∈[0,1],x≤y,都有f(
)=(1-a2)f(x)+a2f(y),其中常数a满足0<a<1,求a的值.
| x+y |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:依题意,可求得f(
)=a2,f(
)=a4,继而可求得f(
)=2a2-a4,利用f(
)=f(
)=-2a6+3a4,可得到关于a的方程a2=-2a6+3a4,解之即可.
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| ||||
| 2 |
解答:
解:因为f(
)=f(
)=a2,…2分
f(
)=f(
)=a2f(
)=a4,…4分
f(
)=f(
)=(1-a2)f(
)+a2f(1)=2a2-a4,…6分
所以f(
)=f(
)=(1-a2)f(
)+a2f(
)=-2a6+3a4,…10分
由此得a2=-2a6+3a4,…12分
而0<a<1,所以a=
…14分
| 1 |
| 2 |
| 0+1 |
| 2 |
f(
| 1 |
| 4 |
0+
| ||
| 2 |
| 1 |
| 2 |
f(
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
所以f(
| 1 |
| 2 |
| ||||
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
由此得a2=-2a6+3a4,…12分
而0<a<1,所以a=
| ||
| 2 |
点评:本题考查抽象函数及其应用,求得f(
)=a2是关键,着重考查赋值法的应用,考查等价转化思想与运算求解能力,属于难题.
| 1 |
| 2 |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数f(x)=x5-x-1在下列区间一定有零点的是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |
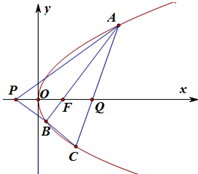 已知抛物线y2=4x的焦点F,过F作直线l交抛物线于A(xA,yA),B(xB,yB)两点,其中点A在x轴上方.
已知抛物线y2=4x的焦点F,过F作直线l交抛物线于A(xA,yA),B(xB,yB)两点,其中点A在x轴上方.