题目内容
已知动点P到定点F（1，0）的距离比到定直线x+2=0的距离少1．
（1）求动点P的轨迹Γ的方程；
（2）设A（横坐标大于1）、B（纵坐标大于0）为轨迹Γ上的相异两点，问是否存在实数λ，使得
=λ
且|AB|=
，若存在，求出λ的值；若不存在，说明理由．
（1）求动点P的轨迹Γ的方程；
（2）设A（横坐标大于1）、B（纵坐标大于0）为轨迹Γ上的相异两点，问是否存在实数λ，使得
| AB |
| AF |
| 16 |
| 3 |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由已知条件得动点P是以F（1，0）为焦点，x=-1为准线的抛物线，由此能求出动点P的轨迹Γ的方程．
（2）假设存在实数λ，使得
=λ
，且|AB|=
，由
=λ
，知A，F，B三点共线，当直线AB斜率不存在时，|AB|=4＜
；当直线AB斜率存在时，设直线AB的方程为y=k（x-1），代入y2=4x，得：k2x2-2（k2+2）x+k2=0，由此利用韦达定理结合已知条件能求出λ的值．
（2）假设存在实数λ，使得
| AB |
| AF |
| 16 |
| 3 |
| AB |
| AF |
| 16 |
| 3 |
解答：
解：（1）根据题意知，动点P到定点F（1，0）的距离等于到直线x+1的距离，
∴动点P是以F（1，0）为焦点，x=-1为准线的抛物线，
∴p=2，动点P的轨迹Γ的方程为y2=4x．
（2）假设存在实数λ，使得
=λ
，且|AB|=
，
由
=λ
，知A，F，B三点共线，
当直线AB斜率不存在时，有A（1，2），B（1，-2），|AB|=4＜
，
当直线AB斜率存在时，设直线AB的方程为y=k（x-1），
代入y2=4x，得：
k2x2-2（k2+2）x+k2=0，
当k=0时，方程只有一解，与题意不符，舍去，
当k≠0时，设A（x1，y1），B（x2，y2），
则x1+x2=
，x1x2=1，
∴|AB|=x1+x2+2=
+2=4+
=
，
解得k=±
，
∵x1＞1，y1＞0，∴k=
，
∴x1=3，x2=
，∴λ=
=
，即?实数λ，使得
=λ
且|AB|=
∴动点P是以F（1，0）为焦点，x=-1为准线的抛物线，
∴p=2，动点P的轨迹Γ的方程为y2=4x．
（2）假设存在实数λ，使得
| AB |
| AF |
| 16 |
| 3 |
由
| AB |
| AF |
当直线AB斜率不存在时，有A（1，2），B（1，-2），|AB|=4＜
| 16 |
| 3 |
当直线AB斜率存在时，设直线AB的方程为y=k（x-1），
代入y2=4x，得：
k2x2-2（k2+2）x+k2=0，
当k=0时，方程只有一解，与题意不符，舍去，
当k≠0时，设A（x1，y1），B（x2，y2），
则x1+x2=
| 2(k2+2) |
| k2 |
∴|AB|=x1+x2+2=
| 2(k2+2) |
| k2 |
| 4 |
| k2 |
| 16 |
| 3 |
解得k=±
| 3 |
∵x1＞1，y1＞0，∴k=
| 3 |
∴x1=3，x2=
| 1 |
| 3 |
| x2-x1 |
| xF-x1 |
| 4 |
| 3 |
| AB |
| AF |
| 16 |
| 3 |
点评：本题考查点的轨迹方程的求法，考查λ的值的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
相关题目
i是虚数单位，
=（ ）
| 3-4i |
| 1+2i |
A、
| ||
B、
| ||
| C、-1+2i | ||
| D、-1-2i |
函数f（x）=x5-x-1在下列区间一定有零点的是（ ）
| A、[0，1] |
| B、[1，2] |
| C、[2，3] |
| D、[3，4] |
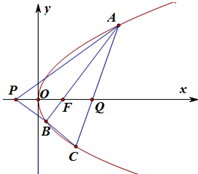已知抛物线y2=4x的焦点F，过F作直线l交抛物线于A（xA，yA），B（xB，yB）两点，其中点A在x轴上方．