题目内容
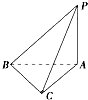
10.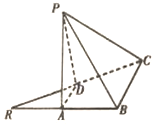 已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.
已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.(1)求C到平面PAB的距离;
(2)求直线PC与平面ABCD成角的正弦值.
分析 (1)根据线面位置关系,可分析出C到平面PAB的距离为线段BC.
(2)连接AC,∠PCA为直线PC与平面ABCD所成角.
解答 解:(1)由题知△RBC为以∠B=90°的等要直角三角形,
∵点A,D分别是RB,RC的中点
∴AD∥BC,即AD⊥BR
将△RAD沿着边AD折起到△PAD位置
∴AD⊥PA,AD⊥AB
∴AD⊥平面PAB
又BC∥AD
∴BC⊥平面PAB
∴C到平面PAB的距离为BC=2
(2)∵PA⊥AB,PA⊥AD
∴PA⊥平面ABCD
∴PC在底面ABCD的投影为AC,
故连接AC.△PAC为RT△.
∵|AC|2=22+12=5,PA=AR=1
∴|PC|2=|AC|2+|PA|2=6
∴$sin∠PCA=\frac{PA}{PC}$=$\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}$.
故直线PC与平面ABCD成角的正弦值为$\frac{\sqrt{6}}{6}$.
点评 考查点面距,线面角的定义及求法(定义法),考查线面位置关系的分析,分析到AD⊥平面PAB;PA⊥平面ABCD是解决问题的关键.本题属于基础题.

练习册系列答案
相关题目
18.已知在△ABC中,c=10,A=45°,C=30°,则a的值为( )
| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{3}$ | C. | 8 | D. | 10 |
5.函数f(x)=$\frac{1}{\sqrt{2-x}}$的定义域为( )
| A. | {x|x<2} | B. | {x|x≤2} | C. | {x|x>2} | D. | {x|x≠2} |
15.若全集 U={x|-2≤x≤2},则集合 A={x|-2≤x≤0}的补集∁U A 为( )
| A. | {x|0<x<2} | B. | {x|0≤x<2} | C. | {x|0<x≤2} | D. | {x|0≤x≤2} |
19.函数f(x)=$\sqrt{1-{{log}_2}x}$的定义域为( )
| A. | (0,+∞) | B. | (0,2) | C. | (2,+∞) | D. | (0,2] |