题目内容
18.已知在△ABC中,c=10,A=45°,C=30°,则a的值为( )| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{3}$ | C. | 8 | D. | 10 |
分析 由已知利用正弦定理即可计算得解.
解答 解:∵c=10,A=45°,C=30°,
∴由正弦定理可得:a=$\frac{csinA}{sinC}$=$\frac{10×\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=10$\sqrt{2}$.
故选:A.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列各组函数中表示同一函数的是( )
| A. | f(x)=x与g(x)=($\sqrt{x}$)2 | B. | f(x)=x|x|与g(x)=$\left\{\begin{array}{l}{{x}^{2}(x>0)}\\{-{x}^{2}(x<0)}\end{array}\right.$ | ||
| C. | f(x)=|x|与g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(t)=t+1(t≠1) |
6.把红、黑、白、蓝4张纸牌随机地分给甲、乙、丙、丁4个人,每个人分得1张,事件“甲分得红牌”与“乙分得红牌”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上均不对 |
13.数列{an}通项an=2-($\frac{x+3}{x}$)n,若$\underset{lim}{n→∞}$an=2,则x的取值范围是( )
| A. | (0,-$\frac{3}{2}$] | B. | (0,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,-$\frac{3}{2}$] |
7.已知数列{an},满足a1=1,an+1=2an+3,则a5等于( )
| A. | 64 | B. | 63 | C. | 32 | D. | 61 |
8.已知集合M={y|y=x2-1,x∈R},P={y|y=2x-1,x∈R},那么集合M与P关系是( )
| A. | M=P | B. | M?P | C. | M?P | D. | P?M |
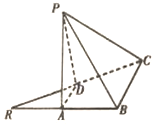 已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.
已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.