题目内容
1.如图,已知PA⊥平面ABC,BC⊥AC,则图中直角三角形的个数为4.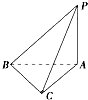
分析 由在Rt△ABC中,∠ACB=90°,P为△ABC所在平面外一点,PA⊥平面ABC,能推导出BC⊥平面PAC.由此能求出四面体P-ABC中有多少个直角三角形.
解答  解:在Rt△ABC中,∠ACB=90°,
解:在Rt△ABC中,∠ACB=90°,
P为△ABC所在平面外一点,PA⊥平面ABC,
∴BC⊥PA,BC⊥AC,
∵PA∩AC=A,
∴BC⊥平面PAC.
∴四面体P-ABC中直角三角形有△PAC,△PAB,△ABC,△PBC.4个.
故答案为:4.
点评 本题考查直线与平面垂直的性质的应用,是基础题.解题时要认真审题,仔细解答,注意等价转化思想的灵活运用.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
11.对任意的实数k,直线y=kx+$\sqrt{3}$与圆x2+y2=4的位置关系一定是( )
| A. | 相离 | B. | 相交但直线过圆心 | ||
| C. | 相切 | D. | 相交但直线不过圆心 |
16.已知集合A={x∈Z|-1<x<3},B={x∈R|x2+x-6<0},则A∩B=( )
| A. | {x|-1<x<2} | B. | {x|-3<x<3} | C. | {0,1} | D. | {0,1,2} |
6.把红、黑、白、蓝4张纸牌随机地分给甲、乙、丙、丁4个人,每个人分得1张,事件“甲分得红牌”与“乙分得红牌”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上均不对 |
13.数列{an}通项an=2-($\frac{x+3}{x}$)n,若$\underset{lim}{n→∞}$an=2,则x的取值范围是( )
| A. | (0,-$\frac{3}{2}$] | B. | (0,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,-$\frac{3}{2}$] |
11.已知向量$\overrightarrow{a}$=(2,x),$\overrightarrow{b}$=(-1,2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的值是( )
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |

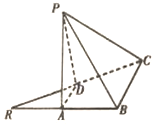 已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.
已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.