题目内容
20.函数f(x)=$\sqrt{x-1}$+$\frac{1}{x-1}$的定义域为{x|x>1}.分析 要使函数f(x)=$\sqrt{x-1}$+$\frac{1}{x-1}$有意义,只需x-1≥0且x-1≠0,解不等式即可得到所求.
解答 解:要使函数f(x)=$\sqrt{x-1}$+$\frac{1}{x-1}$有意义,
只需x-1≥0且x-1≠0,
解得x>1.
则定义域为{x|x>1}.
故答案为:{x|x>1}.
点评 本题考查函数的定义域的求法,注意分式分母不为0,根式偶次式被开方数非负,属于基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(2,x),$\overrightarrow{b}$=(-1,2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的值是( )
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
8.已知集合M={y|y=x2-1,x∈R},P={y|y=2x-1,x∈R},那么集合M与P关系是( )
| A. | M=P | B. | M?P | C. | M?P | D. | P?M |
12.己知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则$\frac{2{S}_{n}+144}{{a}_{n}+5}$的最小值为( )
| A. | 4$\sqrt{19}$-4 | B. | $\frac{27}{2}$ | C. | $\frac{121}{9}$ | D. | $\frac{67}{5}$ |
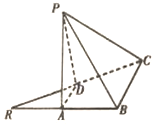 已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.
已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC.