题目内容
3.若函数f(x)=2sinωx(ω>0)的图象在(0,2π)上恰有一个极大值和一个极小值.则ω的取值范围是( )| A. | ($\frac{3}{4}$,1] | B. | (1,$\frac{5}{4}$] | C. | ($\frac{3}{4}$,$\frac{4}{5}$] | D. | ($\frac{3}{4}$,$\frac{5}{4}$] |
分析 根据函数f(x)=2sinωx(ω>0)的图象在(0,2π)恰有一个极大值和一个极小值,结合周期的求法,得$\frac{3}{4}$T<2π≤$\frac{5T}{4}$,由此可得到结论.
解答 解:由题意可得$\frac{3}{4}$T<2π≤$\frac{5T}{4}$,即$\frac{3}{4}$•$\frac{2π}{ω}$<2π≤$\frac{5}{4}$•$\frac{2π}{ω}$,
求得$\frac{3}{4}$<ω≤$\frac{5}{4}$,
故选:D.
点评 本题考查三角函数图象的性质,考查周期的求法,考查学生的计算能力,属于基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.已知函数f(x)=ax3+bx+2015,若f(2016)=4029,则f(-2016)的值为 ( )
| A. | 1 | B. | -4027 | C. | -2014 | D. | 2015 |
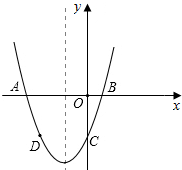 已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.
已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.