题目内容
1.如图1是四棱锥的直观图,其正(主)视图和侧(左)视图均为直角三角形,俯视图外框为矩形,相关数据如图2所示.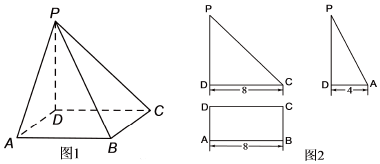
(1)设AB中点为O,在直线PC上找一点E,使得OE∥平面PAD,并说明理由;
(2)若直线PB与底面ABCD所成角的正切值为$\frac{{2\sqrt{5}}}{5}$,求四棱锥P-ABCD的外接球的表面积.
分析 (1)当E是PC中点时,OE∥平面PAD,取PD中点F,连接AF、EF、OF,证明四边形EFAO是平行四边形,即可证明OE∥平面ADP.
(2)由三视图可得PD⊥平面ABCD,连接DB,说明∠PBD是直线PB与底面ABCD所成角,由直观图易知四棱锥P-ABCD的外接球的直径即为PB,求出PB,然后求解四棱锥P-ABCD的外接球的表面积.
解答 解:(1)当E是PC中点时,OE∥平面PAD,
证明如下:取PD中点F,连接AF、EF、OF,
在△PDC中,E、F分别是PC、PD的中点,
∴EF是△PDC的中位线,
∴EF∥DC且$EF=\frac{1}{2}DC$,又O是AB中点,AB=DC,
∴EF∥AO且EF=AO,
∴四边形EFAO是平行四边形,
∴OE∥AF.
又∵AF?平面ADP,OE?平面ADP,
∴OE∥平面ADP.
(2)由三视图可得PD⊥平面ABCD,连接DB,
则∠PBD是直线PB与底面ABCD所成角,
在底面矩形ABCD中,AD=4,AB=8,$DB=4\sqrt{5}$,
∴$tan∠PBD=\frac{PD}{BD}=\frac{PD}{{4\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$,∴PD=8.
由直观图易知四棱锥P-ABCD的外接球的直径即为PB,
∴PB2=PD2+DB2=144.
故四棱锥P-ABCD的外接球的表面积为4πR2=144π.
点评 本题考查几何体的外接球的表面积,直线与平面平行的判断与应用,考查存在性问题,转化思想以及空间想象能力.

练习册系列答案
相关题目
3.设f(x)=e2x-3,g(x)=ln(x+3),则不等式f(g(x))-g(f(x))≤11的解集为( )
| A. | [-5,1] | B. | (-3,1] | C. | [-1,5] | D. | (-3,5] |
16.点M的柱坐标为(4,$\frac{π}{3}$,4),则它的直角坐标为( )
| A. | (-6,$2\sqrt{3}$,4) | B. | (2,$2\sqrt{3}$,4) | C. | (-6,-$2\sqrt{3}$,4) | D. | (-6,$2\sqrt{3}$,-4) |
6.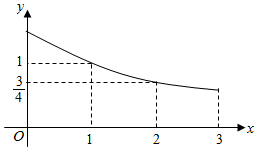 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )| A. | [-2,1] | B. | [-3,-2]∪(0,3] | C. | [-2,0]∪(1,4] | D. | [-3,0]∪[2,5] |
10.要得到函数y=sin2x的图象,只需将函数y=cos2x的图象上的所有点沿x轴( )
| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{2}$个单位长度 |
 如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点. 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.