题目内容
先将函数f(x)=cos(2x+
)的图象上所有的点都向右平移
个单位,再把所有的点的横坐标都伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的解析式和单调递减区间;
(2)若A为三角形的内角,且g(A)=
,求f(
)的值.
| 3π |
| 2 |
| π |
| 12 |
(1)求函数g(x)的解析式和单调递减区间;
(2)若A为三角形的内角,且g(A)=
| 1 |
| 3 |
| A |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性,余弦函数的单调性
专题:三角函数的图像与性质
分析:(1)依题意,易求g(x)=sin(x-
),利用正弦函数的单调性可求得函数g(x)的单调递减区间;
(2)由(1)知,g(A)=sin(A-
)=
,易知0<A-
<
,于是得cos(A-
)=
,f(
)=sinA=sin[(A-
)+
],利用两角和的正弦即可求得答案.
| π |
| 6 |
(2)由(1)知,g(A)=sin(A-
| π |
| 6 |
| 1 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
2
| ||
| 3 |
| A |
| 2 |
| π |
| 6 |
| π |
| 6 |
解答:
解:(1)∵f(x)=cos(2x+
)=sin2x,
∴依题意,有g(x)=sin(x-
),
由
+2kπ≤x-
≤
+2kπ得:
+2kπ≤x≤
+2kπ,k∈Z.
∴g(x)=sin(x-
),且它的单调递减区间为[
+2kπ,
+2kπ]k∈Z.
(2)由(1)知,g(A)=sin(A-
)=
,
∵0<A<π,
∴-
<A-
<
,又0<sin(A-
)<
,
∴0<A-
<
,
∴cos(A-
)=
,
∴f(
)=sinA=sin[(A-
)+
]=
×
+
×
=
.
| 3π |
| 2 |
∴依题意,有g(x)=sin(x-
| π |
| 6 |
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| 2π |
| 3 |
| 5π |
| 3 |
∴g(x)=sin(x-
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 3 |
(2)由(1)知,g(A)=sin(A-
| π |
| 6 |
| 1 |
| 3 |
∵0<A<π,
∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴0<A-
| π |
| 6 |
| π |
| 2 |
∴cos(A-
| π |
| 6 |
2
| ||
| 3 |
∴f(
| A |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||||
| 6 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查正弦函数的单调性,考查诱导公式与两角和的正弦,考查转化思想与综合运算能力,属于中档题.

练习册系列答案
相关题目
若△ABC为锐角三角形,则下列不等式中一定能成立的是( )
A、logcosC
| ||
B、logcosC
| ||
C、logsinC
| ||
D、logsinC
|
设i是虚数单位,复数z1=2-i,z2=1+3i,则z1•z2=( )
| A、-1-5i | B、-1+5i |
| C、5-5i | D、5+5i |
若复数z满足:(3-i)z=3+i(i为虚数单位),则复数z在复平面内对应的点所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
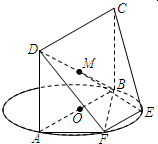 如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=
如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=