题目内容
10．曲线f（x）=x3-x+2在点（1，f（1））处的切线方程为y=2x．分析 求出导数，求得切线的斜率和切点，由点斜式方程可得切线的方程．
解答 解：f（x）=x3-x+2的导数为f′（x）=3x2-1，
即有在点（1，f（1））处的切线斜率为2，切点为（1，2），
则在点（1，f（1））处的切线方程为y-2=2（x-1），
即为y=2x．
故答案为：y=2x．
点评 本题考查导数的运用：求切线的方程，考查直线方程的运用，以及运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
1．袋子中装有大小相同的5个小球，其中有2个红球，3个白球，现从中随机摸出2个小球，则既有红球又有白球的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{7}{10}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |
5．某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．
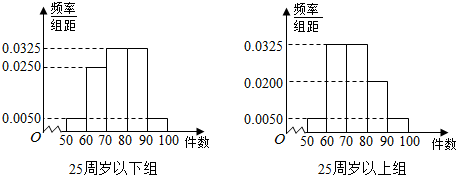
规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？
附表：
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，（其中n=a+b+c+d）
规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？
附表：
| P（K2≥k） | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
15．已知函数$f（x）=\left\{\begin{array}{l}{log_2}x，x＞0\\{2^x}，x≤0\end{array}\right.$，则$f（f（\frac{1}{4}））$的值是（ ）
| A． | $\frac{1}{4}$ | B． | $-\frac{1}{4}$ | C． | 4 | D． | -4 |