题目内容
18．设函数f（x）=alnx+bx2，若函数f（x）的图象在点（1，1）处的切线与y轴垂直，则实数a+b=-1．分析 求出函数的导数，利用函数值以及导函数值，求出a，b即可得到结果．
解答 解：函数f（x）=alnx+bx2，若函数f（x）的图象过（1，1），
可得：b=1，
f′（x）=$\frac{a}{x}$+2x，函数f（x）的图象在点（1，1）处的切线与y轴垂直，
可得a+2=0，
实数a+b=-2+1=-1．
故答案为：-1．
点评 本题考查函数的导数的应用，导数的几何意义，考查计算能力．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
9．函数f（x）=2x+3，则f（-1）=（ ）
| A． | 2 | B． | 1 | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |
6．已知数组（x1，y1），（x2，y2），…，（xn，yn）的线性回归方程是$\hat y=bx+a$，则“x0=$\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$，且y0=$\frac{{{y_1}+{y_2}+…+{y_n}}}{n}$”是“（x0，y0）满足方程$\hat y=bx+a$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
13．
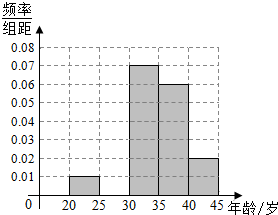由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表所示．
（Ⅰ）求a，b的值；并补全频率分布直方图；
（Ⅱ）根据频率分布直方图估计这507名画师年龄的平均数；
（Ⅲ）在抽出的[20，25）岁的5名画师中有3名男画师，2名女画师．在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？
由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表所示．（Ⅰ）求a，b的值；并补全频率分布直方图；
（Ⅱ）根据频率分布直方图估计这507名画师年龄的平均数；
（Ⅲ）在抽出的[20，25）岁的5名画师中有3名男画师，2名女画师．在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？
| 分组（岁） | 频数 | 频率 |
| [20，25） | 5 | 0.050 |
| [25，30） | a | 0.200 |
| [30，35） | 35 | b |
| [35，40） | 30 | 0.300 |
| [40，45） | 10 | 0.100 |
| 合计 | 100 | 1.00 |
3．从数字1，2，3，4中任取两个不同的数字构成一个两位数，则这个数大于30的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{12}$ |
7．若函数f（x）=|x|+$\sqrt{a-{x^2}}-\sqrt{2}$（a＞0）没有零点，则a的取值范围是（ ）
| A． | $（\sqrt{2}，+∞）$ | B． | （2，+∞） | C． | $（0，1）∪（\sqrt{2}，+∞）$ | D． | （0，1）∪（2，+∞） |