题目内容
13.不等式组$\left\{\begin{array}{l}y-1≥0\\ x-y+2≥0\\ x+4y-8≤0\end{array}\right.$表示的平面区域为Ω,直线x=a(a>1)将Ω分成面积之比为1:4的两部分,则目标函数z=ax+y的最大值为9.分析 由约束条件作出可行域,结合已知求得a,得到线性目标函数,化为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}y-1≥0\\ x-y+2≥0\\ x+4y-8≤0\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{y=1}\\{x+4y-8=0}\end{array}\right.$,解得A(4,1).
联立$\left\{\begin{array}{l}{y=1}\\{x-y+2=0}\end{array}\right.$,解得B(-1,1).
∵直线x=a(a>1)将Ω分成面积之比为1:4的两部分,
∴$\frac{1}{2}(4-a)•(\frac{8-a}{4}-1)=\frac{5}{2}×\frac{1}{5}=\frac{1}{2}$,解得a=2.
∴目标函数z=ax+y=2x+y,化为y=-2x+z,由图可知,
当直线y=-2x+z过A时,直线在y轴上的截距最大,z有最大值为9.
故答案为:9.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{|x|},}&{x≤\frac{1}{2}}\\{\sqrt{2}|lo{g}_{2}x|,}&{x>\frac{1}{2}}\end{array}\right.$,方程f(x)-c=0有四个根,则实数c的取值范围是( )
| A. | [1,$\sqrt{2}$] | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | D. | (1,$\sqrt{2}$) |
1.已知向量$\overrightarrow{a}$=(2,-n),$\overrightarrow{b}$=(Sn,n+1),n∈N*,其中Sn是数列{an}的前n项和,若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则数列{$\frac{{a}_{n}}{{a}_{n+1}{a}_{n+4}}$}的最大项的值为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{2}{3}$ |
18.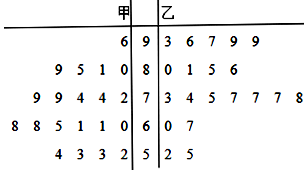 为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
(1)分别计算甲、乙两班20个样本中,数学分数前十的平均分;
(2)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$.(n=a+b+c+d)
独立性检验临界表
 为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.(1)分别计算甲、乙两班20个样本中,数学分数前十的平均分;
(2)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
独立性检验临界表
| P(K2≥0) | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 |
3.△ABC中,$tanA=\frac{3}{4}$,则cos2A等于( )
| A. | $\frac{18}{25}$ | B. | $-\frac{18}{25}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |