题目内容
8.在△ABC中,G点为△ABC的重心,a,b,c分别为角A,B,C的对边,若b2+c2+bc=a2,且S△ABC=2$\sqrt{3}$,则|AG|的最小值为$\frac{2\sqrt{2}}{3}$.分析 b2+c2+bc=a2,可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$-\frac{1}{2}$,A∈(0,π),可得A.利用S△ABC=2$\sqrt{3}$=$\frac{1}{2}bc$sinA,可得bc.设D为BC的中点.由余弦定理可得:(2AD)2+a2=2(b2+c2),利用基本不等式的性质可得:4AD2=b2+c2-bc≥bc=8,再利用AG=2GD即可得出.
解答 解:b2+c2+bc=a2,∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$-\frac{1}{2}$,A∈(0,π),可得A=$\frac{2π}{3}$.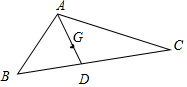
∵S△ABC=2$\sqrt{3}$=$\frac{1}{2}bc$sinA,∴bc=8.①
设D为BC的中点.
由余弦定理可得:(2AD)2+a2=2(b2+c2)②,
∴由①②可得:4AD2=b2+c2-bc≥bc=8,
∴AD的最小值是$\sqrt{2}$,
∵点G为△ABC的重心,AG=2GD.
∴AG的最小值为$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题考查了三角形重心性质、余弦定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
3.等比数列{an}中,S6=120,a1+a3+a5=30,则q=( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
20.当a=16时,如图的算法输出的结果是( )


| A. | 9 | B. | 32 | C. | 10 | D. | 256 |
17.有一段“三段论”推理是这样的“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点;因为函数f(x)=x3在x=0处的导数值f'(x0)=0,所以x=0是函数f(x)=x3的极值点.”以上推理中:(1)大前提错误;(2)小前提错误;(3)推理形式正确;(4)结论正确.你认为正确的序号是( )
| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
18.△ABC中,D为AB的中点,点F在线段CD(不含端点)上,且满足$\overrightarrow{AF}=x\overrightarrow{AB}+y\overrightarrow{AC}$(x,y∈R),则$\frac{1}{x}+\frac{2}{y}$的最小值为( )
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
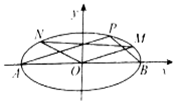 如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.
如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.