题目内容
2.一个算法的程序框图如图,若该程序输出的结果为$\frac{5}{6}$,则判断框中的条件i<m中的整数m的值是6.
分析 首先判断循环结构类型,得到判断框内的语句性质.然后对循环体进行分析,找出循环规律.判断输出结果与循环次数以及i的关系.最终得出结论.
解答 解:第一次循环:S=0+$\frac{1}{1×2}$=$\frac{1}{2}$,i=1+1=2;
第二次循环:S=$\frac{1}{2}$+$\frac{1}{2×3}$=$\frac{4}{6}$,i=2+1=3;
第三次循环:S=$\frac{4}{6}$+$\frac{1}{3×4}$=$\frac{3}{4}$,i=3+1=4;
第四次循环:S=$\frac{3}{4}$+$\frac{1}{4×5}$=$\frac{4}{5}$,i=4+1=5;
第五次循环:S=$\frac{4}{5}$+$\frac{1}{5×6}$=$\frac{5}{6}$,i=5+1=6;输出S,不满足判断框中的条件;
∴判断框中的条件为i<6?
故答案为:6.
点评 本题考查程序框图,尤其考查循环结构.对循环体每次循环需要进行分析并找出内在规律.本题属于基础题

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
12.y=2x关于直线y=x对称的函数为( )
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y={({\frac{1}{2}})^x}$ | C. | y=log2x | D. | y=2-x |
10.执行如图所示的程序框图,若输出的n=6,则输入整数p的最小值是.( )


| A. | 17 | B. | 16 | C. | 18 | D. | 19 |
11.执行如图的程序框图,若输入a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
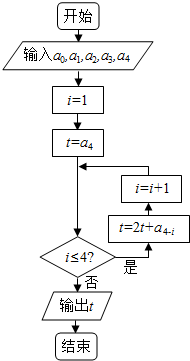

| A. | 5 | B. | 10 | C. | 12 | D. | 14 |
