题目内容
3.执行如图所不的程序框图.输出的结果为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 模拟程序框图的运行过程,计算$\frac{b}{a}$>1时终止循环,求出输出k的值即可.
解答 解:模拟程序框图的运行过程,如下;
b=0,k=1,a=$\frac{2}{3}$,$\frac{b}{a}$=0>1不成立,进行循环;
k=2,b=$\frac{2}{3}$,a=2×${(\frac{2}{3})}^{2}$=$\frac{8}{9}$,$\frac{b}{a}$=$\frac{3}{4}$>1不成立,进行循环;
k=3,b=$\frac{3}{4}$,a=3×${(\frac{2}{3})}^{3}$=$\frac{8}{9}$,$\frac{b}{a}$=$\frac{27}{32}$>1不成立,进行循环;
k=4,b=$\frac{8}{9}$,a=4×${(\frac{2}{3})}^{4}$=$\frac{64}{81}$,$\frac{b}{a}$=$\frac{9}{8}$>1成立,终止循环,输出k=4.
故选:B.
点评 本题考查了程序框图的应用问题,解题时应模拟程序运行的过程,即可得出准确的结论.

练习册系列答案
相关题目
11.执行如图的程序框图,若输入a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
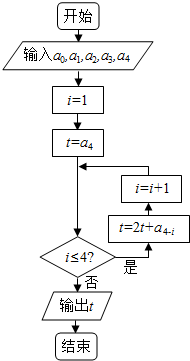

| A. | 5 | B. | 10 | C. | 12 | D. | 14 |
8.执行如图的程序框图,若输入k=100,则输出的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
13.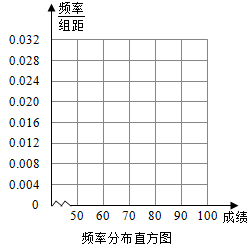 某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:
某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:
(Ⅰ)请根据频率分布表写出a,b,c的值,并完成频率分布直方图;
(Ⅱ)根据(Ⅰ)得到的频率分布直方图估计全校学生成绩的中位数,选择这种数字特征来描述该校学生对安全知识的掌握程度的缺点是什么?
 某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:
某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:| 分组(分数段) | 频数(人数) | 频率 |
| [50,60) | a | 0.08 |
| [60,70) | 13 | 0.26 |
| [70,80) | 16 | 0.32 |
| [80,90) | 10 | 0.20 |
| [90,100) | b | c |
| 合计 | 50 | 1.00 |
(Ⅱ)根据(Ⅰ)得到的频率分布直方图估计全校学生成绩的中位数,选择这种数字特征来描述该校学生对安全知识的掌握程度的缺点是什么?
