题目内容
函数f(x)是R上的奇函数,当x>0时,f(x)=-x2+2x+a(a∈R).
(1)求函数f(x)在(-∞,0)上的单调减区间;
(2)是否存在实数a,使得函数f(x)在[-1,1]上单调递增?若存在,求出a的取值范围,若不存在,请说明理由.
(1)求函数f(x)在(-∞,0)上的单调减区间;
(2)是否存在实数a,使得函数f(x)在[-1,1]上单调递增?若存在,求出a的取值范围,若不存在,请说明理由.
考点:函数奇偶性的性质,函数单调性的性质
专题:计算题,函数的性质及应用
分析:(1)由函数的奇偶性可求得当x∈(-∞,0)时,f(x)=(x+1)2-a-1;从而由二次函数的性质可求函数f(x)在(-∞,0)上的单调减区间为(-∞,-1);
(2)易知函数f(x)在[-1,0)(0,1]上单调递增,从而可得
;从而解得.
(2)易知函数f(x)在[-1,0)(0,1]上单调递增,从而可得
|
解答:
解:(1)当x∈(-∞,0)时,-x>0;
f(x)=-f(-x)=-(-x2-2x+a)
=x2+2x-a=(x+1)2-a-1;
由二次函数的性质知,
函数f(x)在(-∞,0)上的单调减区间为(-∞,-1);
(2)易知函数f(x)在[-1,0)(0,1]上单调递增,
则若使函数f(x)在[-1,1]上单调递增,
则
;
则a≥0.
f(x)=-f(-x)=-(-x2-2x+a)
=x2+2x-a=(x+1)2-a-1;
由二次函数的性质知,
函数f(x)在(-∞,0)上的单调减区间为(-∞,-1);
(2)易知函数f(x)在[-1,0)(0,1]上单调递增,
则若使函数f(x)在[-1,1]上单调递增,
则
|
则a≥0.
点评:本题考查了函数的性质与应用,属于基础题.

练习册系列答案
相关题目
 已知点P(x,y)在如图所示的正六边形P1P2P3P4P5P6区域(含边界)内运动,则当z=4x+5y取到最大值时,点P为于( )
已知点P(x,y)在如图所示的正六边形P1P2P3P4P5P6区域(含边界)内运动,则当z=4x+5y取到最大值时,点P为于( )| A、P1 |
| B、P2 |
| C、P3 |
| D、P4 |
求值:tan42°+tan78°-
tan42°•tan78°=( )
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
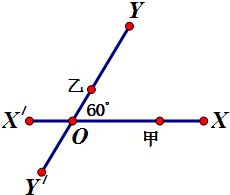 如图,有两条相交成60°角的直路XX′,YY′,交点为O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后来甲沿XX′的方向,乙沿Y′Y的方向,同时以4km/h的速度步行.
如图,有两条相交成60°角的直路XX′,YY′,交点为O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后来甲沿XX′的方向,乙沿Y′Y的方向,同时以4km/h的速度步行.