题目内容
16.已知函数f(x)=$\frac{{\sqrt{3}}}{2}sin(2x+\frac{π}{3})-{cos^2}x+\frac{1}{2}$(x∈R),则下列说法正确的是( )| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | |
| B. | 函数f(x)的图象关于y轴对称 | |
| C. | 点$(\frac{π}{6},0)$为函数f(x)图象的一个对称中心 | |
| D. | 函数f(x)的最大值为$\frac{1}{2}$ |
分析 化函数f(x)为正弦型函数,再依次判断选项中的命题是否正确.
解答 解:函数f(x)=$\frac{{\sqrt{3}}}{2}sin(2x+\frac{π}{3})-{cos^2}x+\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$(sin2xcos$\frac{π}{3}$+cos2xsin$\frac{π}{3}$)-$\frac{1+cos2x}{2}$+$\frac{1}{2}$
=$\frac{\sqrt{3}}{4}$sin2x+$\frac{1}{4}$cos2x
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)(x∈R),
由ω=2知,f(x)的最小正周期为π,A错误;
由f(0)=$\frac{1}{2}$sin$\frac{π}{6}$=$\frac{1}{4}$不是最值,
∴f(x)的图象不关于y轴对称,B错误;
由f($\frac{π}{6}$)=$\frac{1}{2}$sin$\frac{π}{2}$=$\frac{1}{2}$≠0,
∴点$(\frac{π}{6},0)$不是函数f(x)图象的一个对称中心,C错误;
由sin(2x+$\frac{π}{6}$)∈[-1,1],∴f(x)的最大值是$\frac{1}{2}$,D正确.
故选:D.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
4.设等比数列{an}中,若a2=2,a2+a4+a6=14,则公比q=( )
| A. | 3 | B. | $±\sqrt{3}$ | C. | 2 | D. | $±\sqrt{2}$ |
1.某校开设A类选修课3门,B类选修课3门,一位同学 从中选3门.若要求两类课程中各至少选一门,则不同的选法共有( )
| A. | 3种 | B. | 6种 | C. | 9种 | D. | 18种 |
8.已知集合M={x|x2-1≤0},N=|x∈Z|$\frac{1}{2}$<2x+1<4},则M∩N=( )
| A. | {1} | B. | {-1,0} | C. | {-1,0,1} | D. | ∅ |
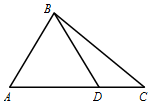 在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,线段AC上点D满足AD=2DC.
在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,线段AC上点D满足AD=2DC.