题目内容
(本小题满分10分)选修4-5:不等式选讲
设函数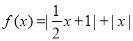
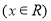 的最小值为a.
的最小值为a.
(1)求a;
(2)已知两个正数m,n满足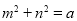 ,求
,求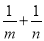 的最小值.
的最小值.
(1)a=1;(2) .
.
【解析】
试题分析:本题主要考查分段函数、函数最值、均值定理等基础知识,同时考查分析问题解决问题的能力、运算求解能力. 第一问,先利用零点分段法去掉绝对值符号,使之转化为分段函数,再根据函数的单调性确定最小值的位置,解出a的值;第二问,利用第一问的结论,两次利用均值不等式计算 的最小值.
的最小值.
试题解析:(Ⅰ) ,
,
当x∈(-∞,0]时,f(x)单调递减,
当x∈[0,+∞)时,f(x)单调递增,
所以当x=0时,f(x)的最小值a=1. …5分
(Ⅱ)由(Ⅰ)知m2+n2=1,由m2+n2≥2mn,得 ,
,
则 ,当且仅当
,当且仅当 时取等号.
时取等号.
所以 的最小值为
的最小值为 . …10分
. …10分
考点:分段函数、函数最值、均值定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,则
,则 的最小值为 .
的最小值为 . 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 . ,被直线
,被直线 :
: 反射,反射光线通过点
反射,反射光线通过点 , 则反射光线所在直线的方程是 .
, 则反射光线所在直线的方程是 . 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 . ,
, ,并得到频率分布直方图(如图),已知测试平均成绩在区间
,并得到频率分布直方图(如图),已知测试平均成绩在区间 有20人.
有20人.
 ,若对于任意
,若对于任意 都有
都有 ,则实数a的取值范围为( )
,则实数a的取值范围为( ) B.
B. C.
C. D.
D.
 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望. 的准线方程为
的准线方程为 。
。 的直线
的直线 与抛物线
与抛物线 相交于
相交于 两点,且以
两点,且以 为直径的圆过原点
为直径的圆过原点 ,求证
,求证 为常数,并求出此常数。
为常数,并求出此常数。