题目内容
已知抛物线 的准线方程为
的准线方程为 。
。
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ) 若过点 的直线
的直线 与抛物线
与抛物线 相交于
相交于 两点,且以
两点,且以 为直径的圆过原点
为直径的圆过原点 ,求证
,求证 为常数,并求出此常数。
为常数,并求出此常数。
(Ⅰ) 
(Ⅱ) 
【解析】
试题分析:
试题解析:(1)由准线方程为 可设抛物线C的方程
可设抛物线C的方程
求得 2分
2分
故所求的抛物线C的方程为: 4分
4分
(2) 依题意可设过P的直线l方程为: (m
(m ), 6分
), 6分
设
由 得:
得:
依题意可知 ,且
,且 8分
8分
原点 落在以
落在以 为直径的圆上
为直径的圆上
令 
即 10分
10分
解得: 即
即 为常数,∴ 原题得证 12分
为常数,∴ 原题得证 12分
(说明:直线l方程也可设为:y=k(x- ),但需加入对斜率不存在情况的讨论,否则扣1分)
),但需加入对斜率不存在情况的讨论,否则扣1分)
考点:抛物线的标准方程,动圆过定点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
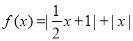
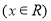 的最小值为a.
的最小值为a.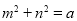 ,求
,求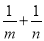 的最小值.
的最小值.
 C.
C. D.2
D.2
 ,
,
 , 其中
, 其中 , 则下列结论中正确的是( )
, 则下列结论中正确的是( ) B.
B. C.
C.  D.
D. 
 的解集是( )
的解集是( ) B.
B. C.
C. D.
D.
 的矩形蔬菜温室.在温室内,沿左、右两端与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左、右两端与后侧内墙各保留1 宽的通道,沿前侧内墙保留2
宽的通道,沿前侧内墙保留2 的图象可能是
的图象可能是

 ,则
,则 是直角三角形”的否命题的真假性为
是直角三角形”的否命题的真假性为  满足
满足 ,
, ,
, ,
, ,则
,则 的最小值为 .
的最小值为 .