题目内容
11.已知集合A={1,2,3},B={1,3},则A∩B=( )| A. | {2} | B. | {1,3} | C. | {1,2} | D. | {1,2,3} |
分析 利用交集定义直接求解.
解答 解:∵集合A={1,2,3},B={1,3},
∴A∩B={1,3}.
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.已知i为虚数单位,则复数$z=\frac{1}{1-i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在极坐标系中,圆ρ=8sinθ上的点到直线θ=$\frac{π}{3}$(ρ∈R)距离的最大值是( )
| A. | -4 | B. | -7 | C. | 1 | D. | 6 |
6.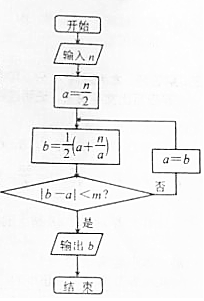 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
1.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{6}x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-ax,恰有三个不同的零点,则a的取值范围是( )
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |