题目内容
已知函数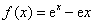 .
.
(Ⅰ)求函数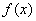 的最小值; (Ⅱ)求证:
的最小值; (Ⅱ)求证: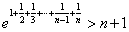
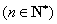 ;
;
(Ⅲ)对于函数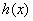 与
与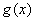 定义域上的任意实数
定义域上的任意实数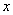 ,若存在常数
,若存在常数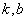 ,使得
,使得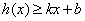 和
和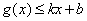 都成立,则称直线
都成立,则称直线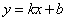 为函数
为函数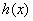 与
与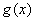 的“分界线”.设函数
的“分界线”.设函数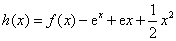 ,
,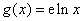 ,
,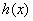 与
与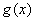 是否存在“分界线”?
是否存在“分界线”?
若存在,求出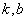 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(Ⅲ)设 .
.
则 .
.
所以当 时,
时, ;当
;当 时,
时, .
.
因此 时
时 取得最小值0,则
取得最小值0,则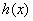 与
与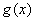 的图象在
的图象在 处有公共点
处有公共点 .
.


练习册系列答案
相关题目
题目内容
已知函数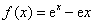 .
.
(Ⅰ)求函数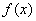 的最小值; (Ⅱ)求证:
的最小值; (Ⅱ)求证: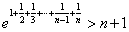
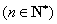 ;
;
(Ⅲ)对于函数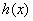 与
与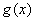 定义域上的任意实数
定义域上的任意实数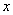 ,若存在常数
,若存在常数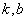 ,使得
,使得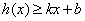 和
和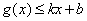 都成立,则称直线
都成立,则称直线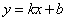 为函数
为函数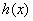 与
与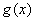 的“分界线”.设函数
的“分界线”.设函数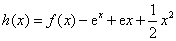 ,
,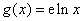 ,
,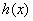 与
与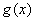 是否存在“分界线”?
是否存在“分界线”?
若存在,求出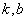 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(Ⅲ)设 .
.
则 .
.
所以当 时,
时, ;当
;当 时,
时, .
.
因此 时
时 取得最小值0,则
取得最小值0,则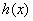 与
与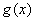 的图象在
的图象在 处有公共点
处有公共点 .
.

