题目内容
已知A,B都是锐角,且A+B≠ ,(1+tan A)(1+tan B)=2,求证:A+B=
,(1+tan A)(1+tan B)=2,求证:A+B=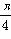 .
.
证明:将(1+tan A)(1+tan B)=2展开得,
1+tan A+tan B+tan Atan B=2,
即tan A+tan B=1-tan Atan B.(*)
因为A+B≠
 ,所以A≠
,所以A≠ -B.因为A,B都是锐角,所以A,
-B.因为A,B都是锐角,所以A, -B都是锐角,从而tan A≠tan
-B都是锐角,从而tan A≠tan .
.
所以tan Atan B≠1,即1-tan Atan B≠0.
(*)式变形得 =1,即tan(A+B)=1,
=1,即tan(A+B)=1,
因为A,B都是锐角,所以0<A+B< ,从而A+B=
,从而A+B= .
.

练习册系列答案
相关题目
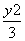 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则 的最小值为( ).
的最小值为( ). C.1 D.0
C.1 D.0 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
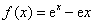 .
.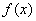 的最小值; (Ⅱ)求证:
的最小值; (Ⅱ)求证: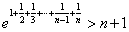
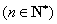 ;
;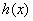 与
与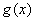 定义域上的任意实数
定义域上的任意实数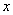 ,若存在常数
,若存在常数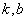 ,使得
,使得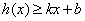 和
和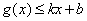 都成立,则称直线
都成立,则称直线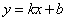 为函数
为函数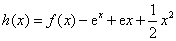 ,
,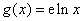 ,
, .
. 导向量的数量积的运算法则:
导向量的数量积的运算法则: ·c=b·c⇒a=b”;
·c=b·c⇒a=b”; 的夹角为
的夹角为 ,且
,且 ,
, ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)