题目内容
已知点M(-3,0)、N(3,0)、B(1,0),动圆C与直线MN相切于点B,分别过点M、N且与圆C相切的两条直线相交于点P,则点P的轨迹方程为( )
A.x2- =1(x>1) B.x2-
=1(x>1) B.x2-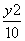 =1(x>0)
=1(x>0)
C.x2- =1(x>0) D.x2-
=1(x>0) D.x2-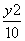 =1(x>1)
=1(x>1)
A
[解析] 如图,设两切线分别与圆相切于点S、T,则|PM|-|PN|=(|PS|+|SM|)-(|PT|+|TN|)=|SM|-|TN|=|BM|-|BN|=2=2a,所以所求曲线为双曲线的右支,∴a=1,c=3,∴b2=8,故点P的轨迹方程为x2- =1(x>0),由题意知,P点不可能与B点重合,∴x>1.
=1(x>0),由题意知,P点不可能与B点重合,∴x>1.


练习册系列答案
相关题目
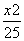 +
+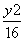 =1的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点距离为________.
=1的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点距离为________.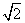 ,在y轴上截得线段长为2
,在y轴上截得线段长为2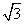 .
.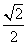 ,求圆P的方程.
,求圆P的方程. 为奇函数,则常数
为奇函数,则常数 = ;
= ; 。
。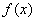 在其定义域上为增函数;
在其定义域上为增函数; ,解关于
,解关于 的不等式
的不等式 。
。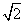 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4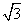 D.4
D.4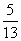 ,焦点在x轴上且长轴长为26.若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
,焦点在x轴上且长轴长为26.若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )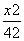 -
-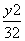 =1 B.
=1 B.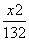 -
-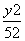 =1
=1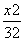 -
-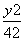 =1 D.
=1 D.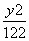 =1
=1