题目内容
原创)已知函数 。
。
(1)用定义证明函数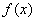 在其定义域上为增函数;
在其定义域上为增函数;
(2)若 ,解关于
,解关于 的不等式
的不等式 。
。
(1)由 得m=1,
得m=1,  。对任
。对任 ,有
,有 ,即
,即 ,
,
故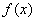 在定义域
在定义域 上为增函数;
上为增函数;
(2)由(1)知, 等价于
等价于 即
即 。
。
当 即
即 时,由于
时,由于 ,此时
,此时 ;
;
当 即
即 时,
时, ;当
;当 即
即 时,
时, ,此时
,此时
所以当 时,不等式解集为
时,不等式解集为 ;当
;当 时;解集为
时;解集为 。
。

练习册系列答案
相关题目
题目内容
原创)已知函数 。
。
(1)用定义证明函数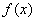 在其定义域上为增函数;
在其定义域上为增函数;
(2)若 ,解关于
,解关于 的不等式
的不等式 。
。
(1)由 得m=1,
得m=1,  。对任
。对任 ,有
,有 ,即
,即 ,
,
故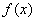 在定义域
在定义域 上为增函数;
上为增函数;
(2)由(1)知, 等价于
等价于 即
即 。
。
当 即
即 时,由于
时,由于 ,此时
,此时 ;
;
当 即
即 时,
时, ;当
;当 即
即 时,
时, ,此时
,此时
所以当 时,不等式解集为
时,不等式解集为 ;当
;当 时;解集为
时;解集为 。
。
