题目内容
14.若(x+$\frac{1}{x}$)(2ax-1)5的展开式中各项系数的和为2,则展开式中的常数项为10.分析 根据展开式中各项系数的和2求得a的值,再把二项式展开,求得该展开式中常数项.
解答 解:∵(x+$\frac{1}{x}$)(2ax-1)5的展开式中各项系数的和为(1+1)(2a-1)5=2,
∴a=1,
∵(2x-1)5的通项为25-rC5rx5-r(-1)r,
当r=4时为10x,
∴(x+$\frac{1}{x}$)(2x-1)5的展开式中的常数项为10x•$\frac{1}{x}$=10,
故答案为:10.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
5.已知集合A={x|y=$\sqrt{2-x}$},B={x|y=log2(x-1)},则A∩B=( )
| A. | {x|0≤x<3} | B. | {x|1<x≤2} | C. | {x|1<x<3} | D. | {x|x≤2} |
9.过点P(-1,3)且平行于直线x-2y+3=0的直线方程为( )
| A. | 2x+y-1=0 | B. | 2x+y-5=0 | C. | x+2y-5=0 | D. | x-2y+7=0 |
19.如图所示的算法中,输出S的值为( )


| A. | 20 | B. | 24 | C. | 33 | D. | 35 |
9. 如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )
如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )
 如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )
如图,在长方形ABCD中,对角线BD与两邻边所成的角分别为α,β则cos2α+cos2β=1.仿此,在长方体ABCD-A′B′C′D′中,下列结论正确的是( )| A. | 若对角线BD′与面ABC,面ABB′,面BCB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=1 | |
| B. | 若对角线BD′与面ABC,面ABB′,面BCB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=2 | |
| C. | 若对角线BD′与三条棱AB,BC,BB′所成的角为α,β,γ,则cos2α+cos2β+cos2γ=2 | |
| D. | 以上类比结论均错误. |
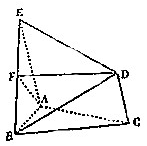 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.