题目内容
4.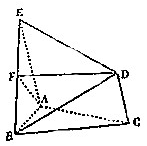 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=4,CD=2,F是BE的中点.(1)求几何体ABCDE的体积;
(2)求证:AF⊥BD.
分析 (1)把三棱锥E-ABD的体积转化为求三棱锥B-AED的体积,然后通过解三角形求得三棱锥B-AED的底面边长和高,则棱锥的体积可求.
(2)由已知条件推导出AF⊥BE,CG⊥AB,DF⊥AB,DF⊥FG,从而AF⊥平面BDF,由此能证明AF⊥BD.
解答  解:(1)∵AB=4,AE=4,CD=2,
解:(1)∵AB=4,AE=4,CD=2,
△ABC是正三角形,∴AC=4
∵AE⊥平面ABC,∴EA⊥AC,
则S△EAD=$\frac{1}{2}$×4×4=8,
又平面EACD⊥面ABC,
在平面ABC内过B作BH⊥AC,则AH⊥面ACDE,
在等边三角形ABC中,求得AH=2$\sqrt{3}$,
∴VE-ABCD=VB-AEDC=$\frac{1}{3}$SAEDC•AH=$\frac{1}{3}×\frac{1}{2}×\frac{4+2}{2}×4×2\sqrt{3}$=4$\sqrt{3}$.
(2)证明:Rt△ABE中,AE=4,AB=4,
F为BE中点,∴AF⊥BE,
∵△ABC是正三角形,∴CG⊥AB,
∴DF⊥AB,
又DF⊥FG,
∴DF⊥平面ABE,DF⊥AF,
∴AF⊥平面BDF,∴AF⊥BD.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
14.已知正实数m,n满足m+n+$\sqrt{{m}^{2}+{n}^{2}}$=2,则mn的最大值为( )
| A. | 6-3$\sqrt{2}$ | B. | 2 | C. | 6-4$\sqrt{2}$ | D. | 3 |
15.已知(1-$\frac{x}{3}$)2015=a0+a1x+…+a2015x2015,则3a1+32a2+…+32015a2015=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 22015-1 |
9.已知5π<θ<6π,设cos$\frac{θ}{2}$=m,则cos$\frac{θ}{4}$等于( )
| A. | $\sqrt{\frac{1-m}{2}}$ | B. | -$\sqrt{\frac{1-m}{2}}$ | C. | $\sqrt{\frac{1+m}{2}}$ | D. | -$\sqrt{\frac{1+m}{2}}$ |
13.已知θ为第二象限角,那么$\frac{θ}{3}$是( )
| A. | 第一或第二象限角 | B. | 第一或四象限角 | ||
| C. | 第二或四象限角 | D. | 第一、二或第四象限角 |
 如图,在△ABC中,C=$\frac{π}{4}$,角B的平分线BD交AC于点D,设∠CBD=θ,其中θ是直线x-2y+3=0的倾斜角.
如图,在△ABC中,C=$\frac{π}{4}$,角B的平分线BD交AC于点D,设∠CBD=θ,其中θ是直线x-2y+3=0的倾斜角. 如图,已知AB是⊙O的直径,C是⊙O上异于A,B的点,VC垂直于⊙O所在的平面,且AB=4,VC=3.
如图,已知AB是⊙O的直径,C是⊙O上异于A,B的点,VC垂直于⊙O所在的平面,且AB=4,VC=3.