题目内容
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线与圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$相切,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 根据题意,由双曲线的方程可得其渐近线方程,由圆的方程可得其圆心坐标以及半径,由双曲线的渐近线与圆相切,则有$\frac{2\sqrt{2}b}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{\frac{8}{3}}$,变形可得3a2=2c2,即$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3}{2}$,由离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,其渐近线方程为y=±$\frac{b}{a}$x,即bx±ay=0,
圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$的圆心为(2$\sqrt{2}$,0),半径为$\sqrt{\frac{8}{3}}$,
若双曲线的渐近线与圆相切,则有$\frac{2\sqrt{2}b}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{\frac{8}{3}}$,
化简可得3a2=2c2,即$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3}{2}$,
则其离心率e=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$;
故选:A.
点评 本题考查双曲线的几何性质,

练习册系列答案
相关题目
9.将周期为π的函数f(x)=2sin(ωx+$\frac{π}{3}$),(ω>0)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.已知D,E是△ABC边BC的三等分点,点P在线段DE上,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则xy的取值范围是( )
| A. | [$\frac{1}{9}$,$\frac{4}{9}$] | B. | [$\frac{1}{9}$,$\frac{1}{4}$] | C. | [$\frac{2}{9}$,$\frac{1}{2}$] | D. | [$\frac{2}{9}$,$\frac{1}{4}$] |
1.若执行如图所示的程序框图,则输出的结果k=( )
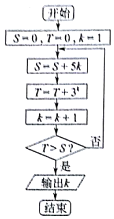

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.下表是某校高三一次月考5个班级的数学、物理的平均成绩:
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
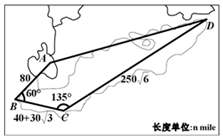 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.