题目内容
16.已知点G是△ABC的重心,过G作BC的平行线与AB,AC分别交于点E,F,若$\overrightarrow{BC}$=$\overrightarrow{a}$,则$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{a}$.分析 如果连接AG并延长,交BC于点P,由三角形的重心的性质可知AG=2GP,则AG:AP=2:3.又EF∥BC,根据相似三角形的判定可知△AGF∽△APC,得出AF:AC=2:3,最后由EF∥BC,得出△AEF∽△ABC,从而求出EF:BC=AF:AC=2:3,问题得以解决.
解答 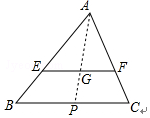 解:如图,连接AG并延长,交BC于点P.
解:如图,连接AG并延长,交BC于点P.
∵G为△ABC的重心,
∴AG=2GP,
∴AG:AP=2:3,
∵EF过点G且EF∥BC,
∴△AGF∽△APC,
∴AF:AC=AG:AP=2:3.
又∵EF∥BC,
∴△AEF∽△ABC,
∴EF:BC=AF:AC=2:3.
∵$\overrightarrow{BC}$=$\overrightarrow{a}$,
∴$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$$\overrightarrow{a}$
故答案为:$\frac{2}{3}$$\overrightarrow{a}$
点评 此题主要考查了三角形的重心的性质,相似三角形的判定及性质,三角形三边的中线相交于一点,这点叫做三角形的重心.重心到顶点的距离等于它到对边中点距离的两倍,平行于三角形一边的直线截其它两边,所得三角形与原三角形相似,相似三角形的三边对应成比例,以及向量的知识.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.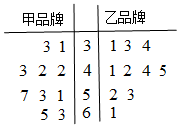 某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
(Ⅰ)现从甲品牌日销量大于40且小于60的样本中任取两天,求这两天都是“畅销日”的概率;
(Ⅱ)用抽取的样本估计这100天的销售情况,请完成这两种品牌100天销量的2×2列联表,并判断是否有99%的把握认为品牌与“畅销日”天数有关.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.(Ⅰ)现从甲品牌日销量大于40且小于60的样本中任取两天,求这两天都是“畅销日”的概率;
(Ⅱ)用抽取的样本估计这100天的销售情况,请完成这两种品牌100天销量的2×2列联表,并判断是否有99%的把握认为品牌与“畅销日”天数有关.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
4.函数$f(x)=\sqrt{x-1}+lg({x+1})$的定义域是( )
| A. | (-1,1] | B. | (-1,1) | C. | [-1,1] | D. | [1,+∞) |
1.全集U=R,集合A={-1,0,1},B={x|$\frac{x-2}{x+1}$>0},则A∩(∁UB)=( )
| A. | {0,1} | B. | {0,1,2} | C. | {-1,0,1} | D. | ∅ |
8.已知直线$y=\frac{{2\sqrt{3}}}{3}x$和椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$交于不同的两点M,N,若M,N在x轴上的射影恰好为椭圆的两个焦点,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
5.定积分${∫}_{0}^{1}$(x+sinx)dx的值为( )
| A. | $\frac{3}{2}$-cos1 | B. | $\frac{{π}^{2}}{2}$+1 | C. | π | D. | $\frac{1}{2}$ |
6.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 12 | B. | 18 | C. | 20 | D. | 24 |