题目内容

1．全集U=R，集合A={-1，0，1}，B={x|$\frac{x-2}{x+1}$＞0}，则A∩（∁UB）=（　　）
A．{0，1}B．{0，1，2}C．{-1，0，1}D．∅

分析 先求出B，再求出C∪B，由此能求出A∩（∁UB）．

解答 解：∵全集U=R，集合A={-1，0，1}，
B={x|$\frac{x-2}{x+1}$＞0}={x|x＜-1或x＞0}，
∴C∪B={x|-1≤x≤0}，
A∩（∁UB）={-1，0，1}．
故选：C．

点评 本题考查的知识点是集合的交集，补集运算，集合的包含关系判断及应用，难度不大，属于基础题．

练习册系列答案
相关题目
11．已知不共线的向量$\overrightarrow a，\overrightarrow b，|{\overrightarrow a}|=2，|{\overrightarrow b}|=3，\overrightarrow a•（{\overrightarrow b-\overrightarrow a}）=1$，则$|{\overrightarrow a-\overrightarrow b}|$=（　　）
A．$\sqrt{3}$B．$2\sqrt{2}$C．$\sqrt{7}$D．$\sqrt{23}$
12．给出如下命题：
①“在△ABC中，若sinA=sinB，则A=B”为真命题；
②若动点P到两定点F1（-4，0），F2（4，0）的距离之和为8，则动点P的轨迹为线段；
③若p∧q为假命题，则p，q都是假命题；
④设x∈R，则“x2-3x＞0”是“x＞4”的必要不充分条件；
⑤若实数1，m，9成等比数列，则圆锥曲线$\frac{x^2}{m}+{y^2}=1$的离心率为$\frac{{\sqrt{6}}}{3}$．
其中，所有正确的命题序号为①②④．
9．已知△ABC在正方形网格中的位置如图所示，则cos∠ABC=（　　）
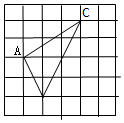
A．$\frac{3}{10}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$
16．已知点G是△ABC的重心，过G作BC的平行线与AB，AC分别交于点E，F，若$\overrightarrow{BC}$=$\overrightarrow{a}$，则$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{a}$．
6．方程log5x+x-2=0的根所在的区间是（　　）
A．（2，3）B．（1，2）C．（3，4）D．（0，1）
13．设$f（x）=3sin\frac{x}{2}-2cos\frac{x}{2}$，将函数y=f（x）的图象上所有点向右平移$\frac{π}{3}$个单位得到函数y=g（x）的图象，若函数g（x）的最大值为g（θ），则$cos（{θ+\frac{π}{6}}）$为-$\frac{12}{13}$．
10．观察下列各式：55=3125，56=15625，57=78125，…，则52017的末四位数字为（　　）
A．3125B．5625C．0625D．8125
11．已知集合A={2，4，6，8}，B={x|3≤x≤6}，则A∩B=（　　）
A．{2，4}B．{4，6}C．{6，8}D．{3，4，6}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网