题目内容
11.某校高三(5)班的一次数学小测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题: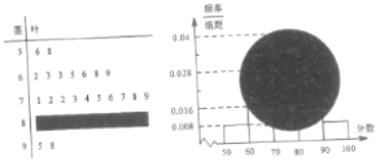
(1)求全班人数,并计算频率分布直方图中[80,90]间的矩形的高;
(2)若要从分数在[80,100]之间的试卷中任选三份来分析学生失分情况,其中u表示分数在[80,90]之间被选上的人数,v表示分数在之[90,100]间被选上的人数,记变量ξ=u-v,求ξ的分布列和期望.
分析 (1)由茎叶图、频率分布直方图,分别求出分数在[50,60)之间的频数和频率,由此能求出全班人数,进而能求出分数在[80,90)之间的频数,由此能求出频率分布直方图中[80,90)间的矩形的高.
(2)μ=3,v=0时,ξ=3,P(ξ=3)=$\frac{1}{5}$,μ=2,v=1时,ξ=1,P(ξ=1)=$\frac{3}{5}$,μ=1,v=2时,ξ=-1,P(ξ=-1)=$\frac{1}{5}$,由此能求出ξ的分布列和期望.
解答 解:(1)由茎叶图、频率分布直方图,知:
分数在[50,60)之间的频率为2,频率为0.008×10=0.08,
∴全班人数为:$\frac{2}{0.08}=25$,
∴分数在[80,90)之间的频数为25-2-7-10-2=4,
频率分布直方图中[80,90)间的矩形的高为$\frac{4}{25}÷10$=0.016.
(2)μ=3,v=0时,ξ=3,P(ξ=3)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
μ=2,v=1时,ξ=1,P(ξ=1)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
μ=2,v=2时,ξ=-1,P(ξ=-1)=$\frac{{C}_{4}^{1}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴ξ的分布列为:
| ξ | -1 | 1 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查茎叶图、频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
1.设x,y∈R,则x>y>0是|x|>|y|的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
2.命题p:?x∈R,|x|≥0,则¬p是( )
| A. | ?x°∈R,|x°|<0 | B. | ?x°∈R,|x°|≥0 | C. | ?x°∈R,|x°|≥0 | D. | ?x∈R,|x|<0 |
19.设函数f(x)=2lnx-x2,则( )
| A. | x=e为极大值点 | B. | x=1为极大值点 | C. | x=1为极小值点 | D. | 无极值点 |
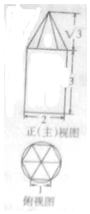 某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.
某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.