题目内容
20.设(2-x)5=a0+a1x+a2x2+…+a5x5,则$\frac{{a}_{2}+{a}_{4}}{{a}_{1}+{a}_{3}}$的值为( )| A. | -$\frac{61}{60}$ | B. | -$\frac{122}{121}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{90}{121}$ |
分析 利用二项式展开式的通项公式求出a1、a2、a3、a4的值,再计算$\frac{{a}_{2}+{a}_{4}}{{a}_{1}+{a}_{3}}$.
解答 解:由(2-x)5=a0+a1x+a2x2+…+a5x5,
且二项式展开式的通项公式为Tr+1=${C}_{5}^{r}$•25-r•(-x)r,
∴a1=-${C}_{5}^{1}$•24=-80,
a2=${C}_{5}^{2}$•23=80,
a3=-${C}_{5}^{3}$•22=-40,
a4=${C}_{5}^{4}$•2=10;
∴$\frac{{a}_{2}+{a}_{4}}{{a}_{1}+{a}_{3}}$=$\frac{80+10}{-80-40}$=-$\frac{3}{4}$.
故选C.
点评 本题考查了二项式展开式通项公式的应用问题,是基础题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
10.已知x,y是[0,1]上的两个随机数,则x,y满足y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
11.已知函数f(x)=|lnx|,$g(x)=\left\{\begin{array}{l}0,0<x≤1\\|{x^2}-4|-2,x>1\end{array}\right.$若方程|f(x)+g(x)|=a有4个实根,则a的取值范围是( )
| A. | (0,1] | B. | (0,2-ln2) | C. | [1,2-ln2] | D. | [1,2-ln2) |
15.已知a、b∈R,则“ab=1”是“直线“ax+y-l=0和直线x+by-1=0平行”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
5.已知向量$\overrightarrow{OA}=({3,1}),\overrightarrow{OB}=({-1,3})$,$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}({m>0,n>0})$,若m+n=1,则$|{\overrightarrow{OC}}$|的最小值为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
12.角α的终边经过的一点P的坐标是(-$\sqrt{3}$,a),则“|a|=1”的充要条件是( )
| A. | $sinα=\frac{1}{2}$ | B. | $cosα=-\frac{{\sqrt{3}}}{2}$ | C. | $tanα=-\frac{{\sqrt{3}}}{3}$ | D. | $|PO|=\sqrt{3}+1$ |
9.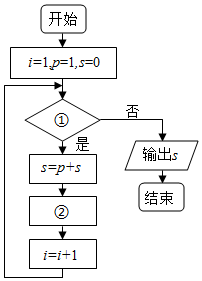 给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
 给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )| A. | i≤40?;p=p+i-1 | B. | i≤41?;p=p+i-1 | C. | i≤41?;p=p+i | D. | i≤40?;p=p+i |
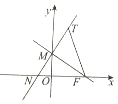 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.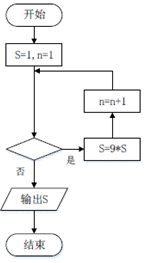 我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )
我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )