已知$\frac{4+mi}{1+2i}$∈R.且m∈R.则|m+6i|=( )A．6B．8C．8$\sqrt{3}$D．10 题目和参考答案——青夏教育精英家教网—

题目内容

14．已知$\frac{4+mi}{1+2i}$∈R，且m∈R，则|m+6i|=（　　）

A．

B．

C．

8$\sqrt{3}$

D．

分析利用两个复数相除，分子和分母同时乘以分母的共轭复数，化简复数为 a+bi的形式，由虚部为0，求得m的值，最后复数求模．

解答解：∵复数$\frac{4+mi}{1+2i}$=$\frac{（4+mi）（1-2i）}{（1+2i）（1-2i）}$=$\frac{4+2m+（m-8）i}{5}$=$\frac{2m+4}{5}$i，
因为复数$\frac{4+mi}{1+2i}$∈R，故m=8，
|m+6i|=|8+6i|=10，
故选 D．

点评本题考查复数是实数的概念、复数求模，本题考查两个复数代数形式的除法，两个复数相除，分子和分母同时乘以分母的共轭复数．转化为a+bi的形式．

练习册系列答案

相关题目

4．在△ABC中，a²=b²+c²-bc，则A等于（　　）

5．已知抛物线x²=y，点A，B在该抛物线上且位于y轴的两侧，且直线AB与y轴交于点（0，a），若∠AOB为锐角（其中O为坐标原点），则实数a的取值范围是（1，+∞）．

2．实数a，b，c不全为0等价于为（　　）

	A．	a，b，c均不为0		B．	a，b，c中至多有一个为0
	C．	a，b，c中至少有一个为0		D．	a，b，c中至少有一个不为0

9．

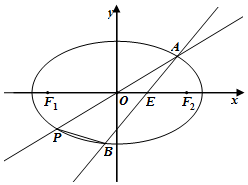如图，在平面直角坐标系xoy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{\sqrt{6}}{3}$，a=$\sqrt{6}$，直线l与x轴交于点E，与椭圆C交于A、B两点．
（1）求椭圆C的方程；
（2）若点E的坐标为（$\frac{\sqrt{3}}{2}$，0），点A在第一象限且横坐标为$\sqrt{3}$，连结点A与原点O的直线交椭圆C于另一点P，求△PAE的面积；
（3）x轴上存在定点E，使得$\frac{1}{E{A}^{2}}$+$\frac{1}{E{B}^{2}}$恒为定值，请指出定点E的坐标，并说明理由．

19．已知直线l₁：y=2x，直线l：y=3x+3．求l₁关于l对称的直线l₂的方程．

6．（1）若tanα=2，求$\frac{sin（2π-α）+cos（π+α）}{{cos（α-π）-cos（\frac{3π}{2}-α）}}$的值
（2）化简：$sin50°（1+\sqrt{3}tan10°）$．

3．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁_UB）∪A为（　　）

4．已知a＞b＞0，c≠0，则下列不等式中不恒成立的是（　　）

（a+b）（ $\frac{1}{a}$+$\frac{1}{b}$）＞4

D．

a²+b²+2＞2a+2b

试题分类