题目内容
已知向量
=(2sinx,sinx-cosx),
=(cosx,
(cosx+sinx)),函数f(x)=
•
+1
(1)当x∈(
,
)时,求f(x)的值域;并求其对称中心.
(2)设△ABC的内角A,B,C所对的边长分别为a,b,c,若将f(x)向左平移
个单位,且b=5,f(
)=3,求△ABC面积最大值.
| a |
| b |
| 3 |
| a |
| b |
(1)当x∈(
| π |
| 4 |
| π |
| 2 |
(2)设△ABC的内角A,B,C所对的边长分别为a,b,c,若将f(x)向左平移
| π |
| 4 |
| B |
| 2 |
考点:两角和与差的正弦函数,平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)求出函数f(x)的表达式,即可求出函数的值域和对称中心.
(2)根据正弦定理以及三角形的面积公式即可得到结论.
(2)根据正弦定理以及三角形的面积公式即可得到结论.
解答:
解:(1)f(x)=sin2x-
cos2x+1=2sin(2x-
)+1,
∵
<x<
,
∴
<2x<π,
∴
<2x-
<
,
∴
<sin(2x-
)≤1,
∴1<2sin(2x-
)≤2,
于是2<2sin(2x-
)+1≤3,
∴f(x)的值域为(2,3],
对称中心(
+
,1).
(2)f(x)=2sin(2x-
)+1平移后f(x)=2sin(2x+
)+1,
∵f(
)=3,
∴2sin(B+
)+1=3,
∴sin(B+
)=1,B=
.
据余弦定理a2+c2-ac=25≥ac,
∴ac≤25,
∴s△=
ac≤
.
| 3 |
| π |
| 3 |
∵
| π |
| 4 |
| π |
| 2 |
∴
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 3 |
∴1<2sin(2x-
| π |
| 3 |
于是2<2sin(2x-
| π |
| 3 |
∴f(x)的值域为(2,3],
对称中心(
| kπ |
| 2 |
| π |
| 6 |
(2)f(x)=2sin(2x-
| π |
| 3 |
| π |
| 6 |
∵f(
| B |
| 2 |
∴2sin(B+
| π |
| 6 |
∴sin(B+
| π |
| 6 |
| π |
| 3 |
据余弦定理a2+c2-ac=25≥ac,
∴ac≤25,
∴s△=
| ||
| 4 |
25
| ||
| 4 |
点评:本题主要考查三角函数的图象和性质,以及余弦定理的应用,考查学生的计算能力.

练习册系列答案
相关题目
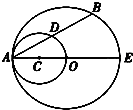 如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.
如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.