题目内容
函数f（x）=3ax2-2ax+1（x∈R）在（-1，1）内有一个零点，则实数a的取值范围是 ．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：利用二次函数的图象和性质进行分析，主要是分函数与x轴相切、相交两种情况判断．
解答：
解：显然a=0时不符合题意．
（1）当△=4a2-12a=0，即a=3或0，对称轴x=
∈(-1，1)成立．但a=0时，不满足，舍去．
（2）当△≠0，要满足题意，即f（-1）f（1）=（5a+1）（a+1）＜0，即a∈(-1，-
)．
综上：所求a的范围是（-1，-
）∪{3}．
（1）当△=4a2-12a=0，即a=3或0，对称轴x=
| 1 |
| 3 |
（2）当△≠0，要满足题意，即f（-1）f（1）=（5a+1）（a+1）＜0，即a∈(-1，-
| 1 |
| 5 |
综上：所求a的范围是（-1，-
| 1 |
| 5 |
点评：本题考查了函数零点的概念，以及二次函数的图象和性质，要注意抓住二次函数的图象特征进行分析．
练习册系列答案
相关题目
已知曲线C：
-
=1的左、右顶点分别为A1，A2，点P在C上且直线PA2斜率的取值范围是[-2，-1]，那么直线PA1斜率的取值范围是（ ）
| x2 |
| 4 |
| y2 |
| 6 |
A、[-1，-
| ||||
B、[-
| ||||
C、[-1，-
| ||||
D、[-
|
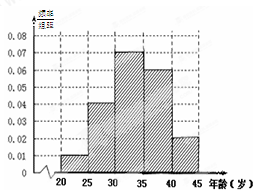上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．根据如图所示的频率分布直方图，估计这507个画师中年龄不超过30岁的人数约已知f（x）=
，x∈R，求f（
）+f（
）+f（
）+…+f（
）=（ ）
| 4x |
| 4x+2 |
| 1 |
| 1001 |
| 2 |
| 1001 |
| 3 |
| 1001 |
| 1000 |
| 1001 |
| A、499.5 | B、500.5 |
| C、500 | D、499 |
