题目内容
20.已知向量$\overrightarrow{a}$=(1,2),向量$\overrightarrow{b}$=(2,m),若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,则实数m的值为-$\frac{7}{2}$.分析 根据平面向量的坐标表示与运算法则,再根据向量垂直时数量积为0,列出方程即可求出实数m的值.
解答 解:∵向量$\overrightarrow{a}$=(1,2),向量$\overrightarrow{b}$=(2,m),
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(3,2+m),
又$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=0,
即1×3+2(2+m)=0,
解得m=-$\frac{7}{2}$.
故答案为:$-\frac{7}{2}$.
点评 本题考查了平面向量的坐标运算与数量积运算的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
 如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |
11. 一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
 一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
一个几何体的三视图如图所示,其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
8.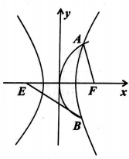 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )| A. | 4-$\sqrt{7}$ | B. | 4-$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 4+$\sqrt{7}$ |
5.已知{an}为等差数列,3a4+a8=36,则{an}的前9项和S9=( )
| A. | 9 | B. | 17 | C. | 36 | D. | 81 |