题目内容
已知函数f(x)=alnx-x2,在区间(0,1)内任取两个实数m,n,且m≠n,不等式ln
>0恒成立,求实数a的取值范围.
| f(m+1)-f(n+1) |
| m-n |
考点:函数恒成立问题
专题:函数的性质及应用
分析:不等式ln
>0恒成立?
>1恒成立,由于
=
,表示点(m+1,f(m+1)) 与点(n+1,f(n+1))连线的斜率,所以函数图象上在区间(1,2)内任意两点连线的斜率大于1,根据导数的几何意义,可将问题转化为在(1,2)上f′(x)=
-2x>1,从而可求出实数a的取值范围.
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
| a |
| x |
解答:
解:由于
=
,
表示点(m+1,f(m+1)) 与点(n+1,f(n+1))连线的斜率,
因实数m,n在区间(0,1)内,故m+1和n+1在区间(1,2)内.
∵不等式ln
>0恒成立?
>1恒成立,
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
∵f(x)=alnx-x2,
∴f′(x)=
-2x,
又函数f′(x)=
-2x在(1,2)上单调递减,
∴在(1,2)上f′(x)=
-2x>1?f′(2)≥1,
即a≥6,
故答案为:a≥6.
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
表示点(m+1,f(m+1)) 与点(n+1,f(n+1))连线的斜率,
因实数m,n在区间(0,1)内,故m+1和n+1在区间(1,2)内.
∵不等式ln
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
∵f(x)=alnx-x2,
∴f′(x)=
| a |
| x |
又函数f′(x)=
| a |
| x |
∴在(1,2)上f′(x)=
| a |
| x |
即a≥6,
故答案为:a≥6.
点评:本题考查函数的性质,导数的几何意义,斜率的概念等知识的灵活应用,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
对正整数m的3次幂进行如下方式的“分裂”:

仿此规律,若m3的“分裂”中最小的数是211,则m的值是( )

仿此规律,若m3的“分裂”中最小的数是211,则m的值是( )
| A、13 | B、15 | C、17 | D、19 |
P是椭圆
+
=1(a>b>0)上的一个点,F为该椭圆的左焦点,O为坐标原点,且△POF为正三角形.则该椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||||
B、2-
| ||||
C、
| ||||
D、
|
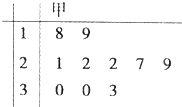 某篮球运动员甲参加了10场比赛,他每场比赛得分的茎叶图如图所示,
某篮球运动员甲参加了10场比赛,他每场比赛得分的茎叶图如图所示,则数据落在区间[22,30)内的概率为( )
| A、0.6 | B、0.5 |
| C、0.4 | D、0.3 |