题目内容
10．某公司生产一种产品，每年需投入固定成本25万元，此外每生产100件这样的产品，还需增加投入50万元，经市场调查知这种产品年需求量为500件，产品销售数量为t件时，销售所得的收入为$（5t-\frac{1}{200}{t}^{2}）$万元．（1）该公司这种产品的年生产量为x件，生产并销售这种产品所得到的利润关于当年产量x的函数为f（x），求f（x）；
（2）当该公司的年产量为多少件时，当年所获得的利润最大？
分析 （1）根据销售这种产品所得的年利润=销售所得的收入-销售成本，建立函数关系即可；
（2）利用配方法，求得0＜x≤500时，$f（x）=-\frac{1}{200}{（x-450）}^{2}+\frac{1975}{2}$在x=450时取得最大值，x＞500时，$f（x）＜-\frac{1}{2}×500+1225=975$，即获得的利润最大．
解答 解：（1）当0＜x≤500时，$f（x）=5x-\frac{1}{200}{x}^{2}-50•\frac{x}{100}-25$．
当x＞500时，$f（x）=5×500-\frac{1}{200}×{500}^{2}-50×\frac{x}{100}-25$，
故$f（x）=\left\{\begin{array}{l}-\frac{1}{200}{x}^{2}+\frac{9x}{2}-250＜x≤500\\-\frac{1}{2}x+1225x＞500\end{array}\right.$；
（2）当0＜x≤500时，$f（x）=-\frac{1}{200}{（x-450）}^{2}+\frac{1975}{2}$
故当x=450时，${f（x）}_{max}=\frac{1975}{2}$；
当x＞500时，$f（x）＜-\frac{1}{2}×500+1225=975$，
故当该公司的年产量为450件时，当年获得的利润最大．
点评 本题考查了函数模型的性质与运用，考查了简单的建模思想方法，训练里利用配方法求二次函数的最值，是中档题．
练习册系列答案
相关题目
1．已知抛物线M：y2=12x的焦点F到双曲线C：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）渐近线的距离为$\frac{3\sqrt{10}}{4}$，点P是抛物线M上的一动点，且P到双曲线C的焦点F1（0，c）的距离与到直线x=-3的距离之和的最小值为5，则双曲线C的方程为（ ）
| A． | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 | B． | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 | C． | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{10}$=1 | D． | $\frac{{y}^{2}}{10}$-$\frac{{x}^{2}}{6}$=1 |
5．已知球O的一个内接三棱锥P-ABC，其中△ABC是边长为2的正三角形，PC为球O的直径，且PC=4，则此三棱锥的体积为（ ）
| A． | $\frac{2}{3}\sqrt{3}$ | B． | $\frac{4}{3}\sqrt{2}$ | C． | $\frac{4}{3}\sqrt{6}$ | D． | $\frac{2}{3}\sqrt{6}$ |
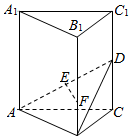在正三棱柱ABC-A1B1C1中，AB=AA1=1，DC=DC1，AE=ED，F为BB1上任意一点，且FB1=3BF．
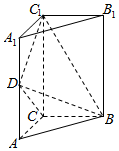如图，底面是直角三角形的直三棱柱ABC-A1B1C1中，$AC=BC=\frac{1}{2}A{A_1}=1$，D是棱AA1上的动点．