题目内容
已知过点A(-4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B,C两点.当直线l的斜率是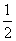 时,
时, =4
=4 .
.
(1)求抛物线G的方程;
(2)设线段BC的中垂线在y轴上的截距为b,求b的取值范围.
解:(1)设B(x1,y1),C(x2,y2),当直线l的斜率为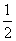 时,l的方程为y=
时,l的方程为y=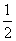 (x+4),即x=2y-4.
(x+4),即x=2y-4.
由 得2y2-(8+p)y+8=0,
得2y2-(8+p)y+8=0,
∴
又∵ =4
=4 ,∴y2=4y1,③
,∴y2=4y1,③
由①②③及p>0得:y1=1,y2=4,p=2,
则抛物线G的方程为x2=4y.
(2)设l:y=k(x+4),
BC的中点坐标为(x0,y0),
由 得x2-4kx-16k=0,④
得x2-4kx-16k=0,④
∴x0= =2k,
=2k,
y0=k(x0+4)=2k2+4k.
∴线段BC的中垂线方程为
y-2k2-4k=- (x-2k),
(x-2k),
∴线段BC的中垂线在y轴上的截距为:
b=2k2+4k+2=2(k+1)2,
对于方程④,由Δ=16k2+64k>0得k>0或k<-4.∴b∈(2,+∞).
故b的取值范围为(2,+∞).

练习册系列答案
相关题目
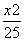 +
+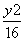 =1的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的距离为( )
=1的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的距离为( )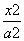 -
-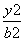 =1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左、右两支分别交于A,B两点.若△ABF2是等边三角形,则该双曲线的离心率为________.
=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左、右两支分别交于A,B两点.若△ABF2是等边三角形,则该双曲线的离心率为________. 是第二象限,
是第二象限, ,则
,则 。
。 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 所对的边,
所对的边, ,
, ,
, ,则
,则 中,若
中,若 ,则
,则 的值等于
的值等于