F1.F2分别是双曲线-＝1(a>0.b>0)的左.右焦点.过F1的直线l与双曲线的左.右两支分别交于A.B两点．若△ABF2是等边三角形.则该双曲线的离心率为．题目和参考答案——青夏教育精英家教网——

题目内容

F₁，F₂分别是双曲线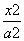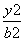－＝1(a>0，b>0)的左、右焦点，过F₁的直线l与双曲线的左、右两支分别交于A，B两点．若△ABF₂是等边三角形，则该双曲线的离心率为________．

解析：如图，由双曲线定义得，|BF₁|－|BF₂|＝

|AF₂|－|AF₁|＝2a，因为△ABF₂是正三角形，所以|BF₂|＝|AF₂|＝

|AB|，因此|AF₁|＝2a，

|AF₂|＝4a，且∠F₁AF₂＝120°，在△F₁AF₂中，4c²＝4a²＋16a²＋2×2a×4a×＝28a²，所以e＝.

练习册系列答案

小学毕业升学全真模拟卷内蒙古人民出版社系列答案

全优假期作业本快乐暑假系列答案

世纪夺冠导航总复习系列答案

海淀黄冈暑假作业合肥工业大学出版社系列答案

快乐暑假快乐学中原农民出版社系列答案

全程解读系列答案

天下无题系列丛书绿色假期暑假作业系列答案

小学生暑假衔接陕西师范大学出版总社系列答案

考易通暑假衔接教材新疆美术摄影出版社系列答案

超能学典暑假接力棒南京大学出版社系列答案

相关题目

已知三个函数f(x)＝2^x＋x，g(x)＝x－2，h(x)＝log₂x＋x的零点依次为a，b，c，则(　　)

A．a<b<c B．a<c<b

C．b<a<c D．c<a<b

圆x²＋y²－2x＋4y－4＝0与直线2tx－y－2－2t＝0(t∈R)的位置关系为(　　)

A．相离　　　　　　　　　 B．相切

C．相交 D．以上都有可能

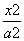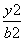已知椭圆＋＝1(a>b>0)，点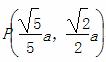在椭圆上．

(1)求椭圆的离心率；

(2)设A为椭圆的左顶点，O为坐标原点，若点Q在椭圆上且满足|AQ|＝|AO|，求直线OQ的斜率．

双曲线x²－my²＝1的实轴长是虚轴长的2倍，则m＝(　　)

A. B.

C．2 D．4

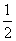抛物线x2＝y的焦点F到其准线l的距离是(　　)

A．2　　　　　　　　　　　 B．1

C. D.

已知过点A(－4,0)的动直线l与抛物线G：x2＝2py(p＞0)相交于B，C两点．当直线l的斜率是时，＝4 .

(1)求抛物线G的方程；

(2)设线段BC的中垂线在y轴上的截距为b，求b的取值范围．

用，，三个不同的字母组成一个含有（）个字母的字符串，要求如下：由字母开始，相邻两个字母不能相同。例如：时，排出的字符串是：，；时，排出的字符串是，，，。在这种含有个字母的所有字符串中，记排在最后一个的字母仍然是的字符串的个数为，得到数列（）。例如：，。记数列（）的前项的和为，则。（用数字回答）

已知全集U ={0，1，2，3，4}，集合是它的子集，

①求；②若=B,求的值；③若，求.