题目内容
12.已知函数f(x)=2lnx-ax,g(x)=x2.(1)若函数f(x)在(2,f(2))处的切线与函数g(x)在(2,g(2))处的切线互相平行,求实数a的值;
(2)设函数H(x)=f(x)-g(x).
(ⅰ)当实数a≥0时,试判断函数y=H(x)在[1,+∞]上的单调性;
(ⅱ)如果x1,x2(x1<x2)是H(x)的两个零点,H'(x)为函数H(x)的导函数,证明:$H'(\frac{{{x_1}+{x_2}}}{2})<0$.
分析 (1)根据导数的几何意义即可求出a的值,
(2)(i)先求导,根据导数和函数的单调性即可判断,
(ii)由H(x)=0,可得H(x1)=2lnx1-x12-ax1=0,H(x2)=2lnx2-x22-ax2=0,通过两式相减,整理化简可得a=$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1),再代入计算可得H′($\frac{{x}_{1}+{x}_{2}}{2}$)=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$],然后换元,构造函数,根据导数和函数的最值即可证明
解答 解:(1)函数f(x)=2lnx-ax的导数为f′(x)=$\frac{2}{x}$-a,
可得f(x)在(2,f(2))处的切线斜率为k1=1-a;
g(x)=x2的导数为g′(x)=2x,
可得函数g(x)在(2,g(2))处的切线斜率为k2=4.
由切线平行,可得1-a=4,
解得a=-3.
(2)(i)H(x)=f(x)-g(x)=2lnx-ax-x2,
∴H′(x)=$\frac{2}{x}$-a-2x=-$\frac{2{x}^{2}+ax-2}{x}$,
易知当x>1时,H′(x)在[1,+∞)上单调递减,
∴H′(x)≤H′(1)=-a,
当a≥0时,H′(x)≤0在[1,+∞)恒成立,
∴当aa≥0时,函数y=H(x)在[1,+∞]上的单调递减,
(ii)∵x1,x2(x1<x2)是H(x)的两个零点,
∴H(x1)=2lnx1-x12-ax1=0,H(x2)=2lnx2-x22-ax2=0,
两式相减可得2ln$\frac{{x}_{2}}{{x}_{1}}$-(x22-x12)-a(x2-x1)=0,
∴a=$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1),
∵H′(x)=$\frac{2}{x}$-a-2x,
∴H′($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{4}{{x}_{1}+{x}_{2}}$-(x2+x1)-[$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-(x2+x1)]=-$\frac{2ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$+$\frac{4}{{x}_{1}+{x}_{2}}$=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$]=-$\frac{2}{{x}_{2}-{x}_{1}}$[2ln$\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$],
不妨设设t=ln$\frac{{x}_{2}}{{x}_{1}}$>1,构造函数h(t)=lnt-$\frac{2(t-1)}{1+t}$,
则h′(t)=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴h(t)在(1,+∞)上是增函数,
∴h(e)>h(1)=0,
∵-$\frac{2}{{x}_{2}-{x}_{1}}$<0,
∴H′($\frac{{x}_{1}+{x}_{2}}{2}$)<0
点评 本题考查了导数的几何意义以及导数和函数的最值,以及函数零点的问题,以及不等式的证明,考查了学生的运算能力和转化能力,属于难题

 名校课堂系列答案
名校课堂系列答案 某几何体三视图如图所示,则该几何体体积为( )
某几何体三视图如图所示,则该几何体体积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
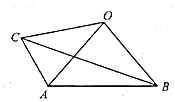 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |