题目内容
1.已知函数f(x)=lnx-ax2在处的切线与直线x-y+1=0垂直.(1)求函数y=f(x)+xf'(x)(f'(x)为f(x)的导函数)的单调区间;
(2)记函数$g(x)=f(x)+\frac{3}{2}{x^2}-({1-b})x$,设x1,x2(x1<x2)是函数g(x)的两个极值点,若$b≥\frac{{{e^2}+1}}{e}-1$,证明:x2≥e.
分析 (1)求出函数f(x)的导函数,由f′(1)=1-2a=-1求得a=1,可得y=f(x)+xf'(x)的解析式,求导后再由导函数分别大于0和小于0求得函数的单调区间;
(2)$g(x)=f(x)+\frac{3}{2}{x^2}-({1-b})x$=$lnx+\frac{1}{2}{x}^{2}-(1+b)x$,求导后利用x1,x2是函数g(x)的两个极值点,可得x1,x2是方程x2-(1+b)x+1=0的两个根,再由根与系数的关系知$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=1+b}\\{{x}_{1}{x}_{2}=1}\end{array}\right.$,进一步得到${x}_{2}+\frac{1}{{x}_{2}}=1+b≥e+\frac{1}{e}$.构造函数h(x)=x+$\frac{1}{x}$,由h(x)在(1,+∞)上单调递增即可证得x2≥e.
解答 (1)解:依题意,f′(x)=$\frac{1}{x}-2ax$,f′(1)=1-2a=-1,得a=1;
又y=f(x)+xf'(x)=lnx-3x2+1,
∴y′=$\frac{1}{x}-6x=\frac{1-6{x}^{2}}{x}$(x>0).
令$y′=\frac{1-6{x}^{2}}{x}$>0,得0<x<$\frac{\sqrt{6}}{6}$;$y′=\frac{1-6{x}^{2}}{x}$<0,得x>$\frac{\sqrt{6}}{6}$.
故函数的单调增区间为(0,$\frac{\sqrt{6}}{6}$),单调减区间为($\frac{\sqrt{6}}{6}$,+∞);
(2)证明:$g(x)=f(x)+\frac{3}{2}{x^2}-({1-b})x$=$lnx+\frac{1}{2}{x}^{2}-(1+b)x$.
g′(x)=$\frac{1}{x}+x-(1+b)=\frac{{x}^{2}-(1+b)x+1}{x}$.
∵x1,x2是函数g(x)的两个极值点,
∴x1,x2是方程x2-(1+b)x+1=0的两个根,
由根与系数的关系知,$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=1+b}\\{{x}_{1}{x}_{2}=1}\end{array}\right.$,
由x1<x2,可知x2>1,又${x}_{2}+\frac{1}{{x}_{2}}=1+b≥e+\frac{1}{e}$.
令h(x)=x+$\frac{1}{x}$,h′(x)=1-$\frac{1}{{x}^{2}}$=$\frac{{x}^{2}-1}{{x}^{2}}$>0(x>1).
∴h(x)在(1,+∞)上单调递增,
由h(x2)≥h(e),得x2≥e.
点评 本题考查利用导数研究函数的单调性,考查了函数极值点与导函数零点关系的应用,考查数学转化思想方法,属中档题.

| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
| A. | 2 | B. | 6 | C. | -1 | D. | -2 |
| A. | {x|x>1} | B. | {x|x<1} | C. | {x|0<x<1} | D. | {x|x>1或x<-1} |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
| A. | [$\frac{3}{2}$,+∞) | B. | (-∞,3)∪(3,+∞) | C. | [$\frac{3}{2}$,3)∪(3,+∞) | D. | (3,+∞) |
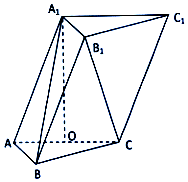 如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.